Question

【题目】设实部为正数的复数z满足，且(1+2i)z在复平面上对应的点在第一、三象限的角平分线上.

（1）求复数z；

（2）若为纯虚数 , 求m的值.

Answer 1

【答案】（1）Z=3－i；（2）－5.

【解析】

（1）设z＝a+bi（a，b∈R且a＞0），由条件可得a2+b2＝10①，a＝﹣3b②．由①②联立的方程组得a、b的值，即可得到z的值．

（2）根据若（m∈R）为纯虚数，可得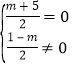，由此求得m的值．

解：（1）设z＝a+bi（a，b∈R且a＞0），由得：a2+b2＝10①．

又复数（1+2i）z＝（a﹣2b）+（2a+b）i在复平面上对应的点在第一、三象限的角平分线上，

则a﹣2b＝2a+b，即a＝﹣3b②．

由①②联立的方程组得a＝3，b＝﹣1；或a＝﹣3，b＝1．

∵a＞0，∴a＝3，b＝﹣1，则z＝3﹣i．

（2）∵ 为纯虚数，∴，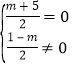

解得m＝﹣5．