题目内容
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是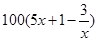 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
(1)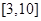 ;(2)以每小时6千克的速度能获得最大利润,最大利润为457500元.
;(2)以每小时6千克的速度能获得最大利润,最大利润为457500元.
解析试题分析:(1)函数应用题是高考的常考内容,一般都是根据题意列出函数式,不等式,方程,而其关系式大多在题目里都有提示,我们只要按照题意列出相应式子,然后根据对应的知识解题即可,如本题就是列出不等式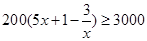 ,这个不等式的解就是所求范围.(2)求利润最大问题,一般是列出函数式,再借助函数的知识解决,本题就是把利润
,这个不等式的解就是所求范围.(2)求利润最大问题,一般是列出函数式,再借助函数的知识解决,本题就是把利润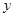 表示为生产速度
表示为生产速度 的函数
的函数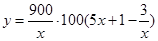 ,这个函数可以看作为关于
,这个函数可以看作为关于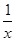 的二次函数,从而可以利用二次函数的知识得解.
的二次函数,从而可以利用二次函数的知识得解.
试题解析:(1)根据题意,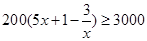
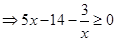 4分
4分
又 ,可解得
,可解得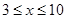 6分
6分
因此,所求 的取值范围是
的取值范围是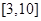 7分
7分
(2)设利润为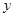 元,则
元,则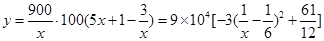 11分
11分
故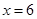 时,
时,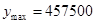 元. 13分
元. 13分
因此该工厂应该以每小时6千克的速度生产才能获得最大利润,最大利润为457500元. 14分
14分
考点:(1)列解不等式;(2)函数的最值.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
;(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于
 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?  的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称. 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.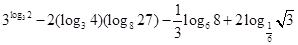 .
.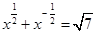 ,求
,求 的值.
的值.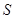 平方米.
平方米.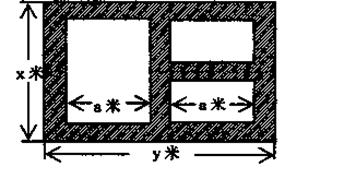
 表示
表示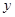 和用
和用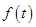 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)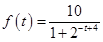 .(设该生物出生时t=0)
.(设该生物出生时t=0)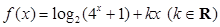 是偶函数。
是偶函数。 的值;
的值;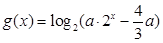 ,其中实数
,其中实数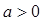 。若函数
。若函数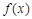 与
与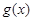 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数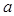 的取值范围。
的取值范围。 ,h(x)=2alnx,
,h(x)=2alnx,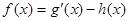 .
. 的单调性;
的单调性;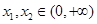 ,且
,且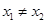 ,都有
,都有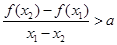
 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛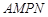 ,要求:B在
,要求:B在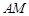 上,D在
上,D在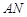 上,对角线
上,对角线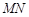 过C点,且矩形
过C点,且矩形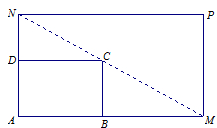
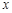 米,矩形
米,矩形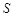 平方米,试用解析式将
平方米,试用解析式将