题目内容
已知函数 ,h(x)=2alnx,
,h(x)=2alnx,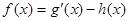 .
.
(1)当a∈R时,讨论函数 的单调性;
的单调性;
(2)是否存在实数a,对任意的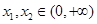 ,且
,且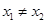 ,都有
,都有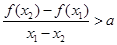
恒成立,若存在,求出a的取值范围;若不存在,说明理由.
(1)详见解析;(2)不存在.
解析试题分析:(1)讨论函数的单调性,在定义域内研究其导函数的符号即可.先求导函数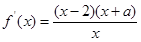
,因为定义域为 ,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点
,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点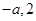 的大小,②注意根与定义域比较,所以
的大小,②注意根与定义域比较,所以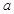 需和-2和0比较大小;(2)由对称性,不妨设
需和-2和0比较大小;(2)由对称性,不妨设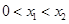 ,去分母得
,去分母得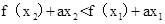 ,构造函数
,构造函数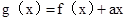 ,则其在定义域内单调递减,故
,则其在定义域内单调递减,故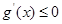 在
在 恒成立,而
恒成立,而 ,分子二次函数开口向上,不可能永远小于0,故不存在.
,分子二次函数开口向上,不可能永远小于0,故不存在.
试题解析:(1)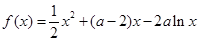 ,∴
,∴ 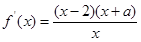 ,
,  的定义域为
的定义域为 .
.
①当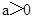 时,
时, 在
在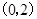 上是减函数,在在
上是减函数,在在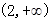 上是增函数;
上是增函数;
②当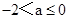 时,
时, 在
在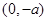 上是增函数;在
上是增函数;在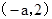 是是减函数;在
是是减函数;在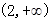 上是增函数;
上是增函数;
③当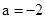 时,
时, 在
在 上是增函数;
上是增函数;
④当 时,
时, 在
在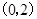 上是增函数;在
上是增函数;在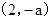 上是减函数;在
上是减函数;在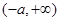 上是增函数.
上是增函数.
(2)假设存在实数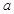 ,对任意的
,对任意的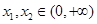 ,且
,且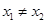 ,都有
,都有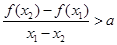 恒成立,不妨设
恒成立,不妨设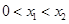 ,要使
,要使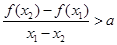 ,即
,即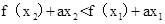 .
.
令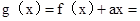
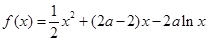 ,只要
,只要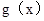 在
在 为减函数.
为减函数.
又 ,由题意
,由题意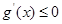 在
在 上恒成立,得
上恒成立,得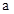 不存在.
不存在.
考点:1、导数在单调性上的应用;2、二次函数的图象;3、函数思想的应用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
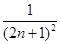 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|< .
. ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是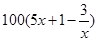 元.
元.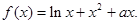
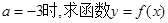 的极值点;
的极值点;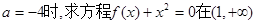 上的根的个数.
上的根的个数.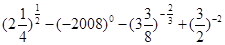
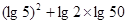
 ,点
,点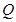 在曲线
在曲线 :
: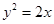 上.
上.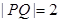 ,求点
,求点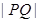 的最小值.
的最小值.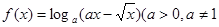 为常数).
为常数). 的定义域;
的定义域;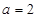 ,
,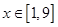 ,求函数
,求函数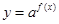 的图像恒在直线
的图像恒在直线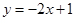 的上方,求实数
的上方,求实数 的取值范围.
的取值范围.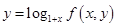 ,
, ,
,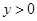 .
.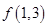 与
与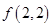 的大小;
的大小; ,证明:
,证明: ;
;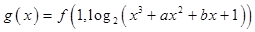 的图象为曲线
的图象为曲线 ,曲线
,曲线 处的切线斜率为
处的切线斜率为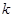 ,若
,若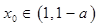 ,且存在实数
,且存在实数 ,使得
,使得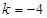 ,求实数
,求实数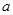 的取值范围.
的取值范围.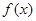 对任意实数
对任意实数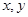 均有
均有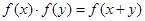 ,且当
,且当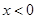 时
时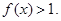
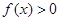 ;
;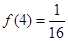 时, 对
时, 对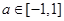 时恒有
时恒有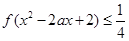 ,求实数
,求实数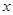 的取值范围.
的取值范围.