题目内容
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
;(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于
 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
(I)y=162-3x(0≤x≤54);(Ⅱ)销售单价为42元/件时,获得最大日销售利润;
解析试题分析:(1)由题意可知 为一次函数,有待定系数法求出解析式;
为一次函数,有待定系数法求出解析式;
(2)销售利润函数=(售价-进价)×销量,代入数值得二次函数,求出最值.
试题解析:(1)因为f(x)为一次函数,设y=ax+b,解方程组 2分
2分
得a=-3,b=162, 4分
故y=162-3x为所求的函数关系式,
又∵y≥0,∴0≤x≤54. 6分
(2)依题意得:
P=(x-30)·y=(x-30)·(162-3x) 8分
=-3(x-42)2+432. 10分
当x=42时,P最大=432,
即销售单价为42元/件时,获得最大日销售利润. 12分
考点:函数模型的选择与应用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 +
+ +
+ +…+
+…+ +
+ +
+ 的值.
的值.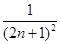 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|< .
.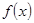 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系: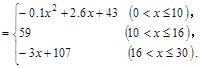
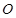 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为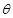 (弧度).
(弧度).
 ,求
,求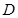 (分贝)由公式
(分贝)由公式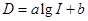 (
(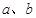 为非零常数)给出,其中
为非零常数)给出,其中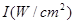 为声音能量.
为声音能量.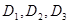 满足
满足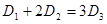 时,求对应的声音能量
时,求对应的声音能量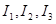 满足的等量关系式;
满足的等量关系式;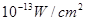 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为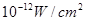 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪. ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是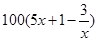 元.
元.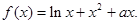
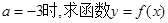 的极值点;
的极值点;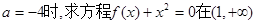 上的根的个数.
上的根的个数.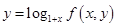 ,
, ,
,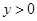 .
.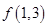 与
与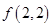 的大小;
的大小; ,证明:
,证明: ;
;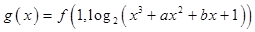 的图象为曲线
的图象为曲线 ,曲线
,曲线 处的切线斜率为
处的切线斜率为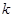 ,若
,若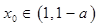 ,且存在实数
,且存在实数 ,使得
,使得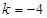 ,求实数
,求实数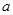 的取值范围.
的取值范围.