题目内容
如图,函数y=f(x)的图象为折线ABC,设f 1 (x)=f(x),f n+1 (x)=f [f n(x)],n∈N*,则函数y=f 4 (x)的图象为

A B C D
D
解析试题分析:函数的图像为折现ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],
由图像可知f(x)为偶函数,关于y轴对称,所以只需考虑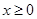 的情况即可.
的情况即可.
由图f1(x)是分段函数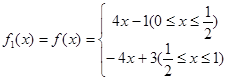 是分段函数,
是分段函数, ,
,
当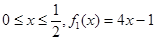 可得
可得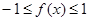 仍然需要进行分类讨论:
仍然需要进行分类讨论:
①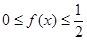 可得
可得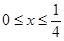 此时f2(x)=f(f1(x))=4(4x-1)=16x-4,
此时f2(x)=f(f1(x))=4(4x-1)=16x-4,
②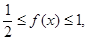 可得
可得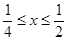 此时f2(x)=f(f1(x))=-4(4x-1)=-16x+4,
此时f2(x)=f(f1(x))=-4(4x-1)=-16x+4,
可得与x轴有2个交点;
当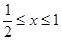 时,也分两种情况,此时也与x轴有两个交点;
时,也分两种情况,此时也与x轴有两个交点;
∴f2(x)在[0,1]上与x轴有4个交点;
那么f3(x)在[0,1]上与x轴有6个交点;
∴f4(x)在[0,1]上与x轴有8个交点,同理在[-1.0]上也有8个交点;故选D
考点:函数的图像
点评:此题主要考查函数的图象问题,以及分段函数的性质及其图象,是一道好题.

将函数 的图像先向左平移2个单位,在向下平移3 个单位后对应的解析式是( )
的图像先向左平移2个单位,在向下平移3 个单位后对应的解析式是( )
A.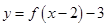 | B. |
C. | D. |
判断下列各组中的两个函数是同一函数的为( )
(1) ,
, ;
;
(2) ,
, ;
;
(3) ,
, ;
;
(4) ,
, .
.
| A.(1),(4) | B.(2),(3) | C.(1) | D.(3) |
下列两个函数为相等函数的是( )
A.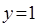 与 与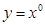 |
B.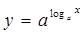 与 与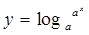 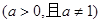 |
C.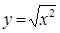 与 与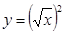 |
D.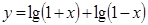 与 与 |
函数 ,则函数
,则函数 的定义域为
的定义域为
A. | B. | C. | D. |
函数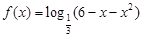 的单调递增区间是
的单调递增区间是
A. | B. | C. | D. |
已知函数 的定义域为R,当
的定义域为R,当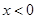 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且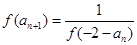 (
( ),则
),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
已知函数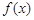 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
 的函数
的函数 ,若存在非零实数
,若存在非零实数 ,使函数
,使函数 和
和 上均有零点,则称
上均有零点,则称


