题目内容
17．
如图，长方体ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形（Ⅰ）在图中画出这个正方形（不必说出画法和理由）
（Ⅱ）求平面α把该长方体分成的两部分体积的比值．
分析 （Ⅰ）利用平面与平面平行的性质，可在图中画出这个正方形；
（Ⅱ）求出MH=$\sqrt{E{H}^{2}-E{M}^{2}}$=6，AH=10，HB=6，即可求平面a把该长方体分成的两部分体积的比值．
解答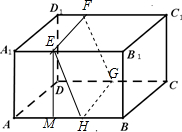 
解：（Ⅰ）交线围成的正方形EFGH如图所示；
（Ⅱ）作EM⊥AB，垂足为M，则AM=A1E=4，EB1=12，EM=AA1=8．
因为EFGH为正方形，所以EH=EF=BC=10，
于是MH=$\sqrt{E{H}^{2}-E{M}^{2}}$=6，AH=10，HB=6．
因为长方体被平面α分成两个高为10的直棱柱，
所以其体积的比值为$\frac{9}{7}$．
点评 本题考查平面与平面平行的性质，考查学生的计算能力，比较基础．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
7．函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（ ）
| A． | （kπ-$\frac{1}{4}$，kπ+$\frac{3}{4}$，），k∈z | B． | （2kπ-$\frac{1}{4}$，2kπ+$\frac{3}{4}$），k∈z | ||
| C． | （k-$\frac{1}{4}$，k+$\frac{3}{4}$），k∈z | D． | （$2k-\frac{1}{4}$，2k+$\frac{3}{4}$），k∈z |
8．命题“?x0∈（0，+∞），lnx0=x0-1”的否定是（ ）
| A． | ?x0∈（0，+∞），lnx0≠x0-1 | B． | ?x0∉（0，+∞），lnx0=x0-1 | ||
| C． | ?x∈（0，+∞），lnx≠x-1 | D． | ?x∉（0，+∞），lnx=x-1 |
2．阅读如图的程序框图，运行相应的程序，则输出S的值为（ ）
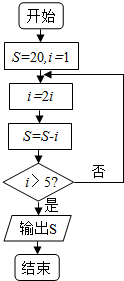
| A． | -10 | B． | 6 | C． | 14 | D． | 18 |
如图，在四棱锥P-ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC=∠BAD=$\frac{π}{2}$，PA=AD=2，AB=BC=1．