题目内容
7.若一个圆锥的侧面展开图恰好是一个半圆,则这个圆锥的侧面积与表面积之比为2:3.分析 根据圆锥体的侧面展开图是半圆,球场底面半径r与母线长l的关系,再求它的侧面积与表面积的比.
解答 解:设该圆锥体的底面半径为r,母线长为l,根据题意得;
2πr=πl,
∴l=2r;
所以这个圆锥的侧面积与表面积的比是
$\frac{1}{2}$πl2:($\frac{1}{2}$πl2+πr2)=$\frac{1}{2}$π(2r)2:($\frac{1}{2}$π(2r)2+πr2)=2:3.
故答案为:2:3.
点评 本题考查了圆锥体的侧面积与底面积的计算问题,也考查了空间想象能力的应用问题,是基础题目.

练习册系列答案
相关题目
12.已知f(x),g(x)都是R上的奇函数,f(x)>0的解集为(a2,b),g(x)>0的解集为($\frac{{a}^{2}}{2}$,$\frac{b}{2}$),且a2<$\frac{b}{2}$,则f(x)•g(x)>0的解集为( )
| A. | (-$\frac{b}{2}$,-a2)∪(a2,$\frac{b}{2}$) | B. | (-$\frac{b}{2}$,a2)∪(-a2,$\frac{b}{2}$) | C. | (-$\frac{b}{2}$,-a2)∪(a2,b) | D. | (-b,-a2)∪(a2,$\frac{b}{2}$) |
19.函数f(x)是奇函数,且在(0,+∞)内是单调递增函数,若f(3)=0,则不等式xf(x)<0的解集是( )
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
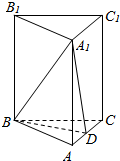 如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点. 如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.
如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD. 如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证:
如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证: