题目内容
12.已知f(x),g(x)都是R上的奇函数,f(x)>0的解集为(a2,b),g(x)>0的解集为($\frac{{a}^{2}}{2}$,$\frac{b}{2}$),且a2<$\frac{b}{2}$,则f(x)•g(x)>0的解集为( )| A. | (-$\frac{b}{2}$,-a2)∪(a2,$\frac{b}{2}$) | B. | (-$\frac{b}{2}$,a2)∪(-a2,$\frac{b}{2}$) | C. | (-$\frac{b}{2}$,-a2)∪(a2,b) | D. | (-b,-a2)∪(a2,$\frac{b}{2}$) |
分析 根据函数奇偶性的性质,求出不等式f(x)<0和g(x)<0的解集,进行求解即可.
解答 解:∵f(x),g(x)都是R上的奇函数,f(x)>0的解集为(a2,b),g(x)>0的解集为($\frac{{a}^{2}}{2}$,$\frac{b}{2}$),且a2<$\frac{b}{2}$,
∴f(x)<0的解集为(-b,-a2),g(x)<0的解集为(-$\frac{b}{2}$,-$\frac{{a}^{2}}{2}$),
则不等式f(x)•g(x)>0等价为$\left\{\begin{array}{l}{f(x)>0}\\{g(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{f(x)<0}\\{g(x)<0}\end{array}\right.$,
即a2<x<$\frac{b}{2}$或-$\frac{b}{2}$<x<-a2,
故不等式的解集为(-$\frac{b}{2}$,-a2)∪(a2,$\frac{b}{2}$),
故选:A.
点评 本题主要考查不等式的求解,根据函数奇偶性的对称性的性质求出f(x)<0和g(x)<0的解集是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.集合A={(x,y)|y=|x|},集合B={(x,y)|y>0,x∈R},则下列说法正确的是( )
| A. | A⊆B | B. | B⊆A | ||
| C. | A∩B=∅ | D. | 集合A、B间没有包含关系 |
1.已知直线l1经过A(-1,4),B(-6,-1)两点,直线l2倾斜角为135°,那么l1与l2( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 相交但不垂直 |
 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.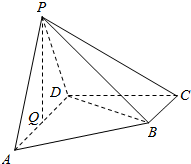 四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.
四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.