题目内容
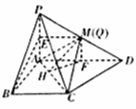
如图,在底面是直角梯形的四棱锥P﹣ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
(Ⅰ) 求证:MC∥平面PAB;
(Ⅱ)在棱PD上找一点Q,使二面角Q﹣AC﹣D的正切值为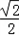 .
.
(Ⅰ) 求证:MC∥平面PAB;
(Ⅱ)在棱PD上找一点Q,使二面角Q﹣AC﹣D的正切值为
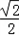 .
.
解:(1)取PA的中点E,连接BE、EM,
则EM与BC平行且相等,
∴四边形BCME是平行四边形.
∴MC∥BE,
又MC 面PAB,BE
面PAB,BE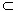 面PAB,
面PAB,
∴MC∥平面PAB
(2)如图过Q作QF∥PA交AD于F,
∴QF⊥平面ABCD.
作FH⊥AC,H为垂足.
连接QH
∴∠QHF是二面角Q﹣AC﹣D的平面角.
设AF=x,
∴AH=FH=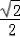 x,
x,
FD=2﹣x.
又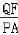 =
=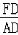 ,
,
∴QF=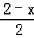 ,
,
在Rt△QFH中,tan∠QHF=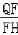 =
=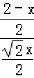 =
= ,
,
∴x=1.当Q为棱PD中点时,二面角Q﹣AC﹣D的正切值为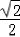 .
.
则EM与BC平行且相等,
∴四边形BCME是平行四边形.
∴MC∥BE,
又MC
 面PAB,BE
面PAB,BE 面PAB,
面PAB,∴MC∥平面PAB
(2)如图过Q作QF∥PA交AD于F,
∴QF⊥平面ABCD.
作FH⊥AC,H为垂足.
连接QH
∴∠QHF是二面角Q﹣AC﹣D的平面角.
设AF=x,
∴AH=FH=
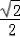 x,
x,FD=2﹣x.
又
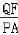 =
=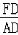 ,
,∴QF=
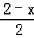 ,
,在Rt△QFH中,tan∠QHF=
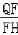 =
=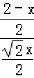 =
= ,
,∴x=1.当Q为棱PD中点时,二面角Q﹣AC﹣D的正切值为
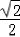 .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
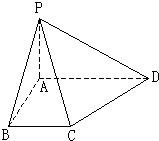 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且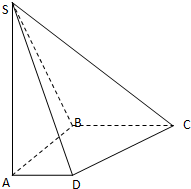 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=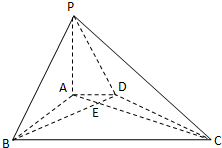 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=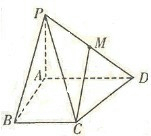 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点. 如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.