题目内容
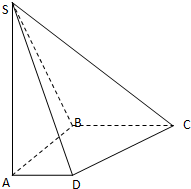 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=| 1 | 2 |
(1)求四棱锥S-ABCD的体积;
(2)求证:面SAB⊥面SBC;
(3)求SC与底面ABCD所成角的正切值.
分析:(1)由题设条四棱锥S-ABCD的体积:V=
Sh=
×
×(AD+BC)×AB×SA,由此能求出结果.
(2)由SA⊥面ABCD,知SA⊥BC,由AB⊥BC,BC⊥面SAB,由此能够证明面SAB⊥面SBC.
(3)连接AC,知∠SCA 就是SC与底面ABCD所成的角.由此能求出 SC与底面ABCD所成角的正切值.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
(2)由SA⊥面ABCD,知SA⊥BC,由AB⊥BC,BC⊥面SAB,由此能够证明面SAB⊥面SBC.
(3)连接AC,知∠SCA 就是SC与底面ABCD所成的角.由此能求出 SC与底面ABCD所成角的正切值.
解答:(1)解:∵底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,
SA⊥面ABCD,SA=AB=BC=1,AD=
.
∴四棱锥S-ABCD的体积:
V=
Sh=
×
×(AD+BC)×AB×SA
=
×(
+1)×1×1=
.
(2)证明:∵SA⊥面ABCD,BC?面ABCD,
∴SA⊥BC,
∵AB⊥BC,SA∩AB=A,
∴BC⊥面SAB
∵BC?面SBC
∴面SAB⊥面SBC.
(3)解:连接AC,
∵SA⊥面ABCD,
∴∠SCA 就是SC与底面ABCD所成的角.
在三角形SCA中,
∵SA=1,AC=
=
,
∴tan∠SCA=
=
=
.…10分
SA⊥面ABCD,SA=AB=BC=1,AD=
| 1 |
| 2 |
∴四棱锥S-ABCD的体积:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)证明:∵SA⊥面ABCD,BC?面ABCD,
∴SA⊥BC,
∵AB⊥BC,SA∩AB=A,
∴BC⊥面SAB
∵BC?面SBC
∴面SAB⊥面SBC.
(3)解:连接AC,
∵SA⊥面ABCD,
∴∠SCA 就是SC与底面ABCD所成的角.
在三角形SCA中,
∵SA=1,AC=
| 12+12 |
| 2 |
∴tan∠SCA=
| SA |
| AC |
| 1 | ||
|
| ||
| 2 |
点评:本题考查棱锥的体积的求法,面面垂直的证明和直线与平面所成角的正切值的求法.解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
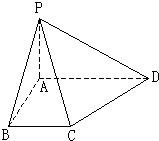 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且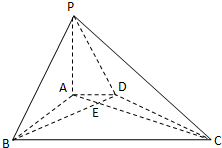 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.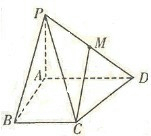 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点. 如图,在底面是直角梯形的四棱锥S-ABCD中,
如图,在底面是直角梯形的四棱锥S-ABCD中,