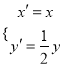题目内容
【题目】在直三棱柱ABC－A1B1C1中，AB＝1，AC＝2，BC＝
，D，E分别是AC1，BB1的中点，则直线DE与平面BB1C1C所成角的正弦值为________．
【答案】
【解析】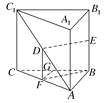
如图，取AC的中点F，连接DF，BF，则DF∥BE，DF＝BE，∴DE∥BF，∴BF与平面BB1C1C所成角的正弦值为所求．∵AB＝1，BC＝
，AC＝2，∴AB⊥BC，又AB⊥BB1，∴AB⊥平面BB1C1C.作GF∥AB交BC于点G，则GF⊥平面BB1C1C，∴∠FBG为直线BF与平面BB1C1C所成的角．由条件知BG＝
BC＝
，GF＝
AB＝
，∴tan∠FBG＝
＝
，∴∠FBG＝
，∴sin∠FBG＝sin
＝
，即直线DE与平面BB1C1C所成角的正弦值为
.
练习册系列答案
相关题目
