题目内容
【题目】已知定义域为![]() 的奇函数
的奇函数![]() .
.
(1)求![]() 的值;
的值;
(2)用函数单调性的定义证明函数![]() 在
在![]() 上是增函数.
上是增函数.
【答案】(1)2;(2)见解析
【解析】试题分析 :(1)利用奇函数定义f(-x)=-f(x)中的特殊值求a的值;
(2)按按取点,作差,变形,判断的过程来即可.
试题解析:(1)∵![]() 是定义域为
是定义域为![]() 的奇函数,
的奇函数,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]()
解得: ![]() .
.
(2)由(1)知, ![]() ,
,
任取![]() ,且
,且![]() ,
,
则![]()
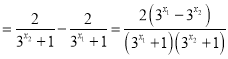
由![]() ,可知:
,可知: ![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴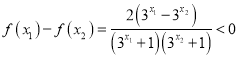 ,即
,即![]() .
.
∴函数![]() 在
在![]() 上是增函数.
上是增函数.
点晴:本题属于对函数单调性应用的考察,若函数![]() 在区间上单调递增,则
在区间上单调递增,则![]() 时,有
时,有![]() ,事实上,若
,事实上,若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,类似地,若
矛盾,类似地,若![]() 在区间上单调递减,则当
在区间上单调递减,则当![]() 时有
时有![]() ;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中可以利用对称性数形结合即可.
;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中可以利用对称性数形结合即可.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目