题目内容
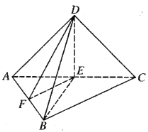
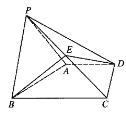
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 与
与![]() 的交点.
的交点.
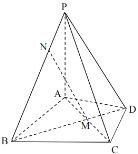
(1)求二面角![]() 的余弦值;
的余弦值;
(2)若点![]() 在线段
在线段![]() 上且
上且![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)在![]() 中,由
中,由![]() 可得
可得![]() ,由余弦定理可得
,由余弦定理可得![]() ,则
,则![]() ,可得
,可得![]() ,以直线
,以直线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,分别求得平面
轴建立空间直角坐标系,分别求得平面![]() 和平面
和平面![]() 的法向量,进而利用向量的数量积求解即可;
的法向量,进而利用向量的数量积求解即可;
(2)先求得平面![]() 的法向量,由点
的法向量,由点![]() 在线段
在线段![]() 上得
上得![]()
![]() ,解得点
,解得点![]() 的坐标,即可得到
的坐标,即可得到![]() ,再由
,再由![]() 求得
求得![]() ,代回
,代回![]() ,进而利用向量的数量积求解即可.
,进而利用向量的数量积求解即可.
(1)在![]() 中,
中,
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() 是等边三角形,则
是等边三角形,则![]() ,
,
所以![]() ,即
,即![]() ,
,
因为![]() 平面
平面![]() ,
,
所以分别以直线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴如图建立空间直角坐标系,
轴如图建立空间直角坐标系,
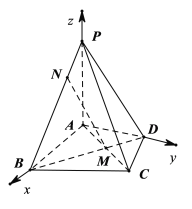
则![]() ,
,![]() ,
,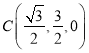 ,
,![]() ,
,![]() ,
,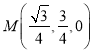 ,
,
则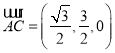 ,
,![]() ,
,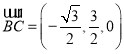 ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即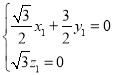 ,
,
令![]() ,则
,则![]() ,
,![]() ,则
,则![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则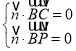 ,即
,即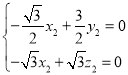 ,
,
令![]() ,则
,则![]() ,
,![]() ,则
,则![]()
则![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]()
(2)设平面![]() 的法向量为
的法向量为![]() ,
,
因为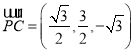 且
且![]() ,
,
则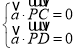 ,即
,即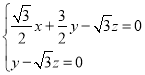 ,
,
令![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
设![]() 且
且![]()
![]() ,
,
则![]() ,即
,即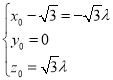 ,则
,则![]() ,
,
所以![]() ,
,
因为![]() ,即
,即![]() ,则
,则![]() ,
,
所以![]() ,
,
因为平面![]() 的法向量
的法向量![]() ,则
,则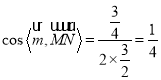 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】我国新型冠状病毒肺炎疫情期间,以网络购物和网上服务所代表的新兴消费展现出了强大的生命力,新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况,在网上随机对1000人做了问卷调查,得如下频数分布表:
网购消费情况(元) |
|
|
|
|
|
频数 | 300 | 400 | 180 | 60 | 60 |
(1)作出这些数据的频率分布直方图,并估计本市居民此期间网络购物的消费平均值;
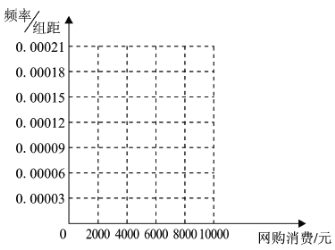
(2)在调查问卷中有一项是填写本人年龄,为研究网购金额和网购人年龄的关系,以网购金额是否超过4000元为标准进行分层抽样,从上述1000人中抽取200人,得到如下列联表,请将表补充完整并根据列联表判断,在此期间是否有95%的把握认为网购金额与网购人年龄有关.
网购不超过4000元 | 网购超过4000元 | 总计 | |
40岁以上 | 75 | 100 | |
40岁以下(含40岁) | |||
总计 | 200 |
参考公式和数据:![]() .(其中
.(其中![]() 为样本容量)
为样本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |