题目内容
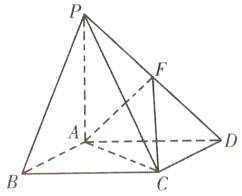
【题目】如图，在三棱锥
中，
，
在底面
上的射影为
，
于点
.
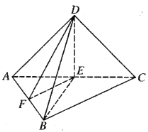
（1）求证：平面
平面
；
（2）若
，求直线
与平面
所成的角的余弦值.
【答案】（1）证明见解析；（2）
.
【解析】
（1）先证明
平面
，又
平面
，从而证明平面
平面；（2）由
平面
，
易知
，则
为
的中点，过点作
于点
，可证
平面
，则
即为
与平面所成的角，最后根据条件和
求出
即可得到结果.
（1）证明：由题意知平面，平面，
所以
，又
，
，所以平面，
又平面，所以平面平面；
（2）由平面，易知
.
则，所以为的中点，
过点作于点，如图：
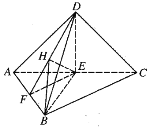
则由（1）知平面平面，又平面
平面
，
则平面，所以即为与平面所成的角，
由
，
得
，
，
又
，且E为AC中点，则
，
中，
，
根据可得，
，
所以
，则
，
所以与平面所成的角的余弦值为.
【点晴】
本题考查面面垂直的证明和线面所成角的求解，几何法求线面所成角关键在于确定高的位置和长度，属中档题.
练习册系列答案
相关题目
【题目】某科研团队对
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
名吸烟患者中，重症人数为
人，重症比例约为
；
名非吸烟患者中，重症人数为
人，重症比例为
.根据以上数据绘制
列联表，如下：
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据，能否在犯错误的概率不超过
的前提下认为新冠肺炎重症和吸烟有关？
(2)已知每例重症患者平均治疗费用约为
万元，每例轻症患者平均治疗费用约为
万元.现有吸烟确诊患者20人，记这
名患者的治疗费用总和为
，求
.
附：
|
|
|
|
|
|
|
|
