题目内容
已知无穷数列{an}中,a1,a2,…,am是首项为10,公差为-2的等差数列;am+1,
am+2,…,a2m是首项为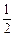 ,公比为
,公比为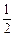 的等比数列(其中 m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.
的等比数列(其中 m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.
(1)当m=12时,求a2010;
(2)若a52=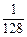 ,试求m的值;
,试求m的值;
(3)判断是否存在m(m≥3,m∈N*),使得S128m+3≥2010成立?若存在,试求出m的值;若不存在,请说明理由.
am+2,…,a2m是首项为
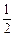 ,公比为
,公比为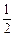 的等比数列(其中 m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.
的等比数列(其中 m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.(1)当m=12时,求a2010;
(2)若a52=
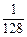 ,试求m的值;
,试求m的值;(3)判断是否存在m(m≥3,m∈N*),使得S128m+3≥2010成立?若存在,试求出m的值;若不存在,请说明理由.
(1)a2010=a18=a12+6=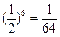 .
.
(2),m=45,或15,或9.
(3)不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.
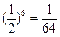 .
.(2),m=45,或15,或9.
(3)不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.
解(1)m=12时,数列的周期为24.
∵2010=24×83+18,而a18是等比数列中的项,
∴a2010=a18=a12+6=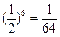 .
.
(2)设am+k是第一个周期中等比数列中的第k项,则am+k=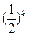 .
.
∵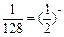 ,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
∴a52最多是第三个周期中的项.
若a52是第一个周期中的项,则a52=am+7=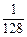 .
.
∴m=52-7=45;
若a52是第二个周期中的项,则a52=a3m+7=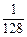 .∴3m=45,m=15;
.∴3m=45,m=15;
若a52是第三个周期中的项,则a52=a5m+7=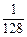 .∴5m=45,m=9;
.∴5m=45,m=9;
综上,m=45,或15,或9.
(3)2m是此数列的周期,
∴S128m+3表示64个周期及等差数列的前3项之和.
∴S2m最大时,S128m+3最大.
∵S2m=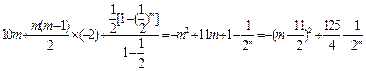 ,
,
当m=6时,S2m=31-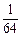 =
=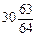 ;
;
当m≤5时,S2m<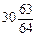 ;
;
当m≤7时,S2m<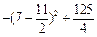 =29<
=29<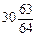 .
.
∴当m=6时,S2m取得最大值,则S128m+3取得最大值为64×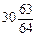 +24=2007.
+24=2007.
由此可知,不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.
∵2010=24×83+18,而a18是等比数列中的项,
∴a2010=a18=a12+6=
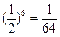 .
.(2)设am+k是第一个周期中等比数列中的第k项,则am+k=
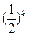 .
.∵
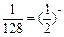 ,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.∴a52最多是第三个周期中的项.
若a52是第一个周期中的项,则a52=am+7=
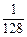 .
.∴m=52-7=45;
若a52是第二个周期中的项,则a52=a3m+7=
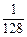 .∴3m=45,m=15;
.∴3m=45,m=15;若a52是第三个周期中的项,则a52=a5m+7=
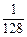 .∴5m=45,m=9;
.∴5m=45,m=9;综上,m=45,或15,或9.
(3)2m是此数列的周期,
∴S128m+3表示64个周期及等差数列的前3项之和.
∴S2m最大时,S128m+3最大.
∵S2m=
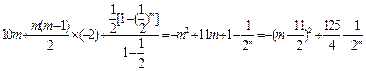 ,
,当m=6时,S2m=31-
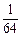 =
=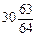 ;
;当m≤5时,S2m<
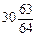 ;
;当m≤7时,S2m<
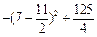 =29<
=29<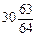 .
.∴当m=6时,S2m取得最大值,则S128m+3取得最大值为64×
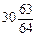 +24=2007.
+24=2007.由此可知,不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
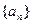 是公差为d的等差数列,其前n项和为Sn,则有
是公差为d的等差数列,其前n项和为Sn,则有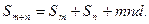 类似的,对于公比为q的等比数列
类似的,对于公比为q的等比数列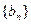 来说,设其前n项积为Tn,则关于
来说,设其前n项积为Tn,则关于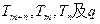 的一个关系式为 。
的一个关系式为 。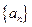 中,
中,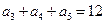 ,那么
,那么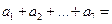 ( )
( )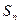 为等比数列
为等比数列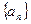 的前n项和,
的前n项和, ,则
,则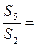 ( )
( )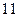

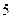
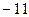
 第6行的第二个数16=5+11,第三个数25=11+14
第6行的第二个数16=5+11,第三个数25=11+14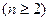 第2个数是 .
第2个数是 . 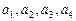 是等差数列,且满足
是等差数列,且满足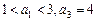 ,若
,若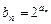 ,给出下列命题:
,给出下列命题: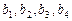 是一个等比数列; (2)
是一个等比数列; (2)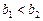 ; (3)
; (3)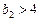 ; (4)
; (4)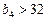 ; (5)
; (5)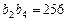 .
.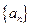 的通项公式为
的通项公式为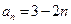 .则它的公差为( )
.则它的公差为( )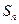 是等差数列
是等差数列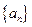 的前
的前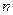 项和,
项和,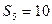 ,则
,则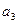 的值为
的值为 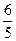
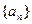 中,已知
中,已知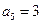 ,
,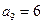 ,则
,则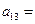 ( )
( )