题目内容
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数,
为参数, ![]() ),将曲线
),将曲线![]() 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线![]() .
.
(1)以原点为极点, ![]() 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() (
(![]() 为参数)与
为参数)与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]()
【解析】【试题分析】(1)先将![]() 的参数方程消参变为直销坐标方程, 把
的参数方程消参变为直销坐标方程, 把![]() 代入上述方程可得到
代入上述方程可得到![]() 的方程,代入极坐标和直角坐标转化公式可求得
的方程,代入极坐标和直角坐标转化公式可求得![]() 的极坐标方程.(2)写出直线
的极坐标方程.(2)写出直线![]() 的极坐标方程,分别代入
的极坐标方程,分别代入![]() 的极坐标方程,求得对应
的极坐标方程,求得对应![]() ,结合
,结合![]() 可求得
可求得![]() 的值.
的值.
【试题解析】
(1)![]() 的普通方程为
的普通方程为![]() ,
,
把![]() 代入上述方程得,
代入上述方程得, ![]() ,
,
∴![]() 的方程为
的方程为![]() ,
,
令![]() ,
,
所以![]() 的极坐标方程为
的极坐标方程为![]() ;
;
(2)在(1)中建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
由![]() ,得
,得![]() ,
,
由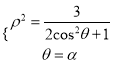 ,得
,得![]() ,
,
而![]() ,∴
,∴![]() ,
,
而![]() ,∴
,∴![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某同学学习习惯不好,把黑板上老师写的表达式忘了,记不清楚是![]() 还是
还是![]() .翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
.翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
| 0 |
|
|
| |
|
|
|
|
| |
| 0 | 3 | 0 | 0 |
(1)请你帮助该同学补充完表格中的数据,写出该函数的表达式![]() ,并写出该函数的最小正周期;
,并写出该函数的最小正周期;
(2)若利用![]() 的图象用图象变化法作
的图象用图象变化法作![]() 的图象,其步骤如下:(在空格内填上合适的变换方法)
的图象,其步骤如下:(在空格内填上合适的变换方法)
第一步:![]() 的图象向右平移
的图象向右平移![]() _____得到
_____得到![]() _____的图象;
_____的图象;
第二步:![]() 的图象(纵坐标不变)______得到
的图象(纵坐标不变)______得到![]() _____的图象;
_____的图象;
第三步:![]() 的图象(横坐标不变)_____得到
的图象(横坐标不变)_____得到![]() 的图象.
的图象.




