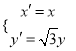题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与
与![]() 相交于A,B两点,
相交于A,B两点,![]() 的周长为
的周长为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 为直角,若存在求出此时直线
为直角,若存在求出此时直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【答案】(1)![]() ;(2)故不存在直线
;(2)故不存在直线![]() 使
使![]() 为直角
为直角
【解析】
(1)由离心率为![]() 得a
得a![]() c,由△F1AB周长为4
c,由△F1AB周长为4![]() 可求得a值,进而求得b值;
可求得a值,进而求得b值;
(2)联立直线和椭圆方程,转化为一元二次方程根与系数之间的关系,利用设而不求思想进行转化求解即可.
(1)∵椭圆离心率为![]() ,∴
,∴![]() ,∴a
,∴a![]() c,
c,
又△F1AB周长为4![]() ,∴4a=4
,∴4a=4![]() ,解得a
,解得a![]() ,∴c=1,b
,∴c=1,b![]() ,
,
∴椭圆C的标准方程为:![]() ;
;
(2)椭圆C的右焦点(1,0),
①当直线l斜率不存在时,直线l与椭圆C交于(![]() ,
,![]() ).(1,
).(1,![]() )两点,显然不存在满足条件的直线.
)两点,显然不存在满足条件的直线.
②当直线l斜率存在时,设直线l:y=kx![]() k代入
k代入![]() ,
,
消y得,(2+3k2)x2-6k2x+3k2﹣6=0,
由于直线l经过椭圆 C左焦点,所以直线l必定与椭圆C有两个交点,
则△>0恒成立
设A(x1,y1),B(x2,y2),则x1+x2![]() ,x1x2
,x1x2![]() ,
,
若![]() 为直角,则
为直角,则![]() 0,即x1x2+y1y2=0 (*)
0,即x1x2+y1y2=0 (*)
而y1y2=(kx1![]() k)(kx2
k)(kx2![]() k)=k2x1x2
k)=k2x1x2![]() k2(x1+x2)+k2,代入(*)式得,
k2(x1+x2)+k2,代入(*)式得,
(1+k2)x1x2![]() k2(x1+x2)+k2=0,
k2(x1+x2)+k2=0,
即(1+k2)![]() k2
k2![]() k2=0,解得k2
k2=0,解得k2![]() ,
,
所以不存在k使得![]() 为直角.
为直角.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目