题目内容
6.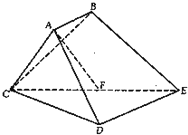 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.(1)求证:AF⊥CD;
(2)求直线AC与平面CBE所成角大小的正弦值.
分析 (1)取CD的中点G,连接AG、GF,由三角形中位线定理可得GF∥DE,再由AC=AD得AG⊥GD,结合已知得到DE⊥CD,即GF⊥CD,最后由线面垂直的判断和性质证得AF⊥CD;
(2)法一、建立空间直角坐标系G-xyz,利用空间向量求出$\overrightarrow{CA}$与平面CBE的法向量所成角的余弦值,从而得到直线AC与平面CBE所成角正弦值;
法二、由线面垂直的性质得AB∥DE,延长DA、EB交于点P,连结PC,可得PC∥AG.进一步得到PC⊥平面CDE.求出点A到平面PCE的距离$h=\frac{{\sqrt{2}}}{2}$.则直线AC与平面CBE所成角的正弦值可求.
解答 (1)证明:取CD的中点G,连接AG、GF,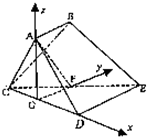
则GF∥DE,
∵AC=AD,∴AG⊥GD,
∵DE⊥平面ACD,∴DE⊥CD,
∴GF⊥CD,
∴CD⊥平面AGF.
∵AF?平面AGF,∴AF⊥CD;
(2)解:法一、如图建立空间直角坐标系G-xyz,
则B(0,1,$\sqrt{3}$),C(-1,0,0),E(1,2,0),
$\overrightarrow{CB}=(1,1,\sqrt{3}),\overrightarrow{CE}=(2,2,0)$$\overrightarrow{CA}=(1,0,\sqrt{3})$,
设平面CBE的法向量为$\overrightarrow{n}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CB}=x+y+\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{CE}=2x+2y=0}\end{array}\right.$,取x=1,则$\overrightarrow{n}=(1,-1,0)$,
∴$cos<\overrightarrow{CA},\overrightarrow{n}>=\frac{\overrightarrow{CA}•\overrightarrow{n}}{|\overrightarrow{CA}|•|\overrightarrow{n}|}=\frac{\sqrt{2}}{4}$.
∴直线AC与平面CBE所成角的大小的正弦值为$\frac{{\sqrt{2}}}{4}$.
解法二、∵AB⊥平面ACD,DE⊥平面ACD,∴AB∥DE.
延长DA、EB交于点P,连结PC,
∵AB=1,DE=2,∴A为PD的中点,
又G为CD的中点,∴PC∥AG.
∴PC⊥CD,PC⊥DE,∴PC⊥平面CDE.
∵点A到平面PCE的距离即为点D到平面PCE的距离的一半,即$h=\frac{{\sqrt{2}}}{2}$.
设直线AC与平面CBE所成角为θ,
则$sinθ=\frac{h}{AC}=\frac{{\sqrt{2}}}{4}$.
点评 本题考查直线和平面垂直的性质,考查了线面角的求法,训练了利用空间向量求解线面角,考查空间想象能力和思维能力,是中档题.

| A. | y=x2-1 | B. | y=x3 | C. | y=ex | D. | y=lnx |
| A. | (1,1.5) | B. | (1.5,2) | C. | (2,3) | D. | 无法确定 |
 如图所示茎叶图记录甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
如图所示茎叶图记录甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分)