题目内容
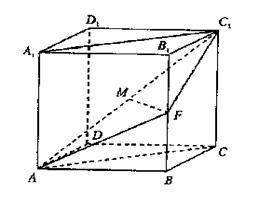
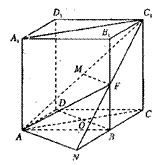
已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点。
(1)求证:直线MF∥平面ABCD;
(2)求平面AFC1与平面ABCD所成二面角的大小。
(1)求证:直线MF∥平面ABCD;
(2)求平面AFC1与平面ABCD所成二面角的大小。

(1)延长C1F交CB的延长线于点N,连接AN。因为F是BB1的中点,所以F为C1N的中点,B为CN的中点。
又M是线段AC1的中点,故MF∥AN。
又MF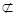 平面ABCD,AN
平面ABCD,AN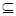 平面ABCD。
平面ABCD。
∴MF∥平面ABCD。
(2)易得BD⊥ACC1A1,又AC1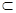 ACC1A1,
ACC1A1,
∴BD⊥AC1,∴BD∥NA,∴AC1⊥NA。
又由BD⊥AC可知NA⊥AC,
∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角。
在Rt△C1AC中,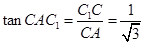 ,
,
故∠C1AC=30°
∴平面AFC1与平面ABCD所成二面角的大小为30°或150°
又M是线段AC1的中点,故MF∥AN。
又MF
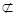 平面ABCD,AN
平面ABCD,AN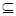 平面ABCD。
平面ABCD。∴MF∥平面ABCD。
(2)易得BD⊥ACC1A1,又AC1
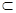 ACC1A1,
ACC1A1,∴BD⊥AC1,∴BD∥NA,∴AC1⊥NA。
又由BD⊥AC可知NA⊥AC,
∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角。
在Rt△C1AC中,
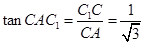 ,
, 故∠C1AC=30°
∴平面AFC1与平面ABCD所成二面角的大小为30°或150°

略

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
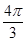 ,则此球的表面积为 .
,则此球的表面积为 .
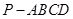 中,底面
中,底面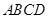 是平行四边形,
是平行四边形,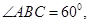
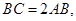
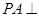 底面
底面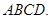
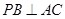 ;(Ⅱ)若
;(Ⅱ)若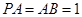 ,求二面角
,求二面角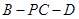 的余弦值;
的余弦值;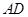 上是否存在一点
上是否存在一点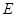 使二面角
使二面角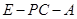 为
为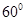 ,若存在,试确定点
,若存在,试确定点
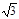
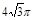

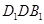 ;
;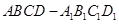 中,
中,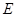 为
为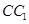 的中点.
的中点.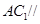 平面
平面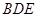 ;
;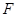 在棱
在棱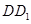 上什么位置时,平面
上什么位置时,平面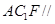 平面
平面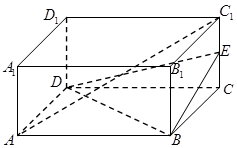
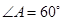 、边长为
、边长为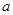 的菱形,又
的菱形,又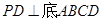 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
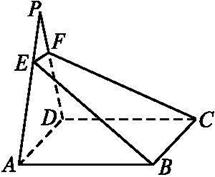
 FE交AP于E,交DP于F.求证:四边形BCFE是梯形.
FE交AP于E,交DP于F.求证:四边形BCFE是梯形.