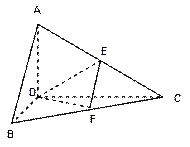
题目内容
(本题满分12分)已知四棱锥P-ABCD,底面ABCD是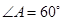 、边长为
、边长为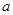 的菱形,又
的菱形,又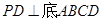 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN//平面PMB;
(2)求DN与MB所成的角的正弦值.

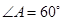 、边长为
、边长为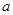 的菱形,又
的菱形,又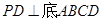 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.(1)证明:DN//平面PMB;
(2)求DN与MB所成的角的正弦值.

(1)证明:取PB中点Q,连结MQ、NQ,
 M、N分别是棱AD、PC中点,
M、N分别是棱AD、PC中点,
∴ QN//BC//MD,且QN=MD,
∴四边形DNQM是平行四边形
于是DN//MQ.
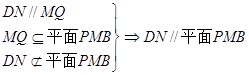 .
.
(2)解:由(1)知DN//MQ,∴ DN与MB所成的角是
由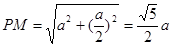 ,
, ,
,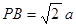
知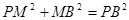 即
即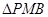 是
是
取MB中点G,连结GQ,有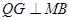 ,且
,且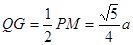
又
故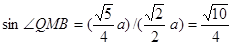 为所求.
为所求.
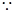 M、N分别是棱AD、PC中点,
M、N分别是棱AD、PC中点,∴ QN//BC//MD,且QN=MD,
∴四边形DNQM是平行四边形
于是DN//MQ.
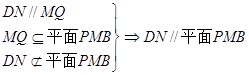 .
.(2)解:由(1)知DN//MQ,∴ DN与MB所成的角是

由
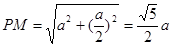 ,
, ,
,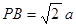
知
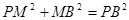 即
即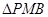 是
是
取MB中点G,连结GQ,有
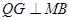 ,且
,且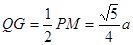
又

故
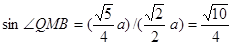 为所求.
为所求.略

练习册系列答案
相关题目
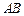 为圆
为圆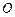 的直径,点
的直径,点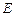 、
、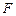 在圆
在圆 ,矩形
,矩形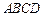 所在的平面和圆
所在的平面和圆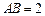 ,
,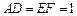 .
.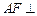 平面
平面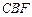 ;
;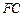 的中点为
的中点为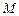 ,求证:
,求证: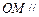 平面
平面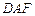 ;
;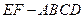 分割成的两个锥体的体积分别为
分割成的两个锥体的体积分别为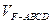 、
、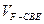 ,求
,求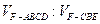 的值
的值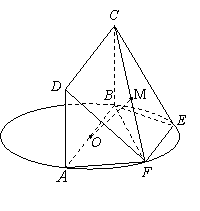
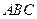 的边长为4,
的边长为4,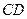 是
是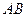 边上的高,
边上的高,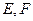 分别是
分别是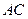 和
和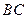 边的中点,现将△
边的中点,现将△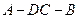 .
.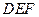 的位置关系,并说明理由;
的位置关系,并说明理由;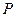 ,使
,使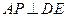 ?证明你的结论.
?证明你的结论.