题目内容
1.已知函数f(x)=$\sqrt{2}$cos(x+$\frac{π}{12}$),x∈R.(1)求f($\frac{7π}{12}$)的值;
(2)若cosθ=$\frac{3}{5}$,θ∈(-$\frac{π}{2}$,0),求f(2θ-$\frac{π}{3}$).
分析 (1)直接利用条件求得f($\frac{7π}{12}$)=$\sqrt{2}$cos$\frac{2π}{3}$ 的值.
(2)由条件求得sinθ的值,可得sin2θ 和cos2θ 的值,从而求得f(2θ-$\frac{π}{3}$)=$\sqrt{2}$cos(2θ-$\frac{π}{3}$+$\frac{π}{12}$)=$\sqrt{2}$cos(2θ-$\frac{π}{4}$)的值.
解答 解:(1)因为函数f(x)=$\sqrt{2}$cos(x+$\frac{π}{12}$),所以f($\frac{7π}{12}$)=$\sqrt{2}$cos$\frac{2π}{3}$=-$\sqrt{2}$cos$\frac{π}{3}$=-$\frac{\sqrt{2}}{2}$.
(2)因为cosθ=$\frac{3}{5}$,θ∈(-$\frac{π}{2}$,0),所以 sinθ=-$\sqrt{{1-cos}^{2}θ}$=-$\frac{4}{5}$.
所以sin2θ=2sinθcosθ=-$\frac{24}{25}$,cos2θ=2cos2θ-1=-$\frac{7}{25}$,
所以f(2θ-$\frac{π}{3}$)=$\sqrt{2}$cos(2θ-$\frac{π}{3}$+$\frac{π}{12}$)=$\sqrt{2}$cos(2θ-$\frac{π}{4}$)=$\sqrt{2}$cos2θcos$\frac{π}{4}$+sin2θsin$\frac{π}{4}$=-$\frac{31}{25}$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式的应用,属于基础题.

练习册系列答案
相关题目
16.过点C(-1,1)和D(1,3),圆心在x轴上的圆的方程是( )
| A. | x2+(y-2)2=10 | B. | x2+(y+2)2=10 | C. | (x-2)2+y2=10 | D. | (x+2)2+y2=10 |
 如图,边长为1正方形ABCD中,分别在边BC、AD上各取一点M与N,下面用随机模拟的方法计算|MN|>1.1的概率.利用计算机中的随机函数产生两个0~1之间的随机实数x,y,设BM=x,AN=y,则可确定M、N点的位置,进而计算线段MN的长度.设x,y组成数对(x,y),经随机模拟产生了20组随机数:
如图,边长为1正方形ABCD中,分别在边BC、AD上各取一点M与N,下面用随机模拟的方法计算|MN|>1.1的概率.利用计算机中的随机函数产生两个0~1之间的随机实数x,y,设BM=x,AN=y,则可确定M、N点的位置,进而计算线段MN的长度.设x,y组成数对(x,y),经随机模拟产生了20组随机数: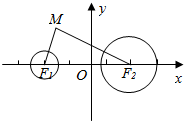 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.