题目内容
6.已知直线m⊥平面α,直线n在平面β内,给出下列四个命题:①α∥β⇒m⊥n;②α⊥β⇒m∥n;③m⊥n⇒α∥β;④m∥n⇒α⊥β,其中真命题的个数是( )| A. | ①② | B. | ①④ | C. | ②③ | D. | ②④ |
分析 由直线与平面垂直的性质定理得到①正确;在②中,m与n相交、平行或异面;在③中,α与β相交或平行;由平面与平面垂直的判定定理得④正确.
解答 解:由直线m⊥平面α,直线n在平面β内,知:
①∵α∥β,∴直线m⊥平面β,∴m⊥n,故①正确;
②α⊥β⇒m与n相交、平行或异面,故②错误;
③m⊥n⇒α与β相交或平行,故③错误;
④∵m∥n,∴由平面与平面垂直的判定定理得α⊥β,故④正确.
故选:B.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用和空间思维能力的培养.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
16.已知函数f(x)=3x-3|x|,若3tf(2t)-mf(t)≥0对于t∈[-2,-1]恒成立,则实数m范围是( )
| A. | [$\frac{1}{9}$,+∞) | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{10}{9}$,+∞) | D. | (-∞,$\frac{10}{9}$] |
17.编号分别为A1,A2,A3,…,A12的12名篮球运动员在某次篮球比赛中的得分记录如下:
(1)完成如下的频率分布表:
(2)从得分在区间[10,20)内的运动员中随机抽取2人,求这2人得分之和大于30的概率.
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 |
| 得分 | 5 | 10 | 12 | 16 | 8 | 21 | 27 | 15 | 6 | 22 | 18 |
| 得分区间 | 频数 | 频率 |
| [0,10) | 3 | $\frac{1}{4}$ |
| [10,20) | ||
| [20,30) | ||
| 合计 | 12 | 1.00 |
14.某几何体的三视图如图所示,则该几何体的体积等于( )
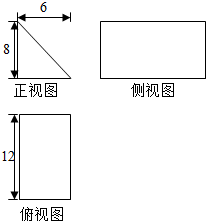

| A. | 576 | B. | 288 | C. | 192 | D. | 144 |