题目内容
9.将函数y=f(x)的图象沿x轴向右平移$\frac{π}{3}$个单位,再保持图象上的纵坐标不变,而横坐标变为原来的2倍,得到的曲线与y=sinx的图象相同,则y=f(x)的解析式是y=sin(2x+$\frac{2π}{3}$).分析 由题意函数y=sinx的图象,逐步逆推求出函数y=f(x)的图象对应的解析式即可.
解答 解:函数y=sinx的图象,将图象上各点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),得到函数y=sin2x,再把它的图象向左平移$\frac{π}{3}$个单位,得到函数y=sin(2x+$\frac{2π}{3}$)的图象.
故答案为:y=sin(2x+$\frac{2π}{3}$).
点评 本题是基础题,考查三角函数的图象的平移,伸缩变换,注意函数变换的形式,逐步可逆,化简解题过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.编号分别为A1,A2,A3,…,A12的12名篮球运动员在某次篮球比赛中的得分记录如下:
(1)完成如下的频率分布表:
(2)从得分在区间[10,20)内的运动员中随机抽取2人,求这2人得分之和大于30的概率.
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 |
| 得分 | 5 | 10 | 12 | 16 | 8 | 21 | 27 | 15 | 6 | 22 | 18 |
| 得分区间 | 频数 | 频率 |
| [0,10) | 3 | $\frac{1}{4}$ |
| [10,20) | ||
| [20,30) | ||
| 合计 | 12 | 1.00 |
14.某几何体的三视图如图所示,则该几何体的体积等于( )
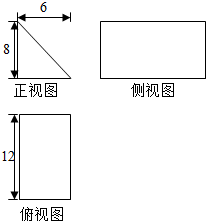

| A. | 576 | B. | 288 | C. | 192 | D. | 144 |
 若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.
若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.