题目内容
5.已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=0处的切线为l:4x+y-5=0,若x=-2时,y=f(x)有极值.(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
分析 (1)先求出函数的导数,得到关于a,b,c的不等式组,解出即可;(2)先求出函数的表达式,求出函数f(x)的导数,从而求出函数的单调区间,函数的最值.
解答 解:(1)由f(x)=x3+ax2+bx+c,
得:f′(x)=3x2+2ax+b,
当x=0时,切线l的斜率为-4,可得b=-4①,
当x=-2时,y=f(x)有极值,得f′(-2)=0,
∴12-4a+b=0②,
由①②得:a=2,b=-4,
由于切点的横坐标为x=0,
∴f(0)=5,∴c=5,
∴a=2,b=-4,c=5.
(2)由(1)得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4,
令f′(x)=0,解得:x=-2或x=$\frac{2}{3}$,
当x变化时,y′,y的值及变化如下表:
| x | -3 | (-3,-2) | -2 | (-2,$\frac{2}{3}$) | $\frac{2}{3}$ | ($\frac{2}{3}$,1) | 1 |
| y′ | + | 0 | - | 0 | + | ||
| y | 8 | 递增 | 13 | 递减 | $\frac{95}{27}$ | 递增 | 4 |
点评 本题考查了函数的单调性,函数的最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
20.若a,b,c∈(0,+∞),且a+b+c=1,则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\root{3}{2}}{3}$ | C. | $\frac{9}{2}$ | D. | $\frac{1}{9}$ |
17.$cos(\frac{19π}{3})$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
14.已知△ABC的三边满足(a+b+c)(a+b-c)=($\sqrt{3}$+2)ab,则角C等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
15.cos(-2640°)+sin1665°=( )
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | -$\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1+\sqrt{2}}}{2}$ | D. | -$\frac{{1+\sqrt{2}}}{2}$ |
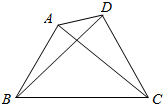 在四边形ABCD中,AB=$\sqrt{3}$,CD=2,∠BAD=135°,∠BCD=60°,∠ADB=30°.
在四边形ABCD中,AB=$\sqrt{3}$,CD=2,∠BAD=135°,∠BCD=60°,∠ADB=30°.