题目内容
15.已知实数p,q,r满足:p+q+r=m,且p2+q2+r2=m(m>0).(1)当r=$\frac{1}{2}$,求m的取值范围;
(2)当m=1,且p,q都不为0,求$\frac{1}{p}$+$\frac{1}{q}$的取值范围;
(3)求m的取值范围.
分析 (1)化简得出pq=$\frac{1}{2}$[m2-2m$+\frac{1}{2}$],p+q=m-$\frac{1}{2}$,构造x2-(m-$\frac{1}{2}$)x$+\frac{1}{2}$[m2-2m$+\frac{1}{2}$]=0的两个不为0的根p,q,运用方程有根得出△=(m-$\frac{1}{2}$)2-4×$\frac{1}{2}$[m2-2m$+\frac{1}{2}$]≥0,即可求解.
(2)p+q=1-r,p2+q2=1-r2,pq=r2-r,化简得出$\frac{1}{p}$+$\frac{1}{q}$=$-\frac{1}{r}$,构造x2-(1-r)x+(r2-r)=0的两个不为0的根p,q,△=(1-r)2-4(r2-r)≥0,得出r的范围,即可求解问题.
(3)平方得出p2+q2+r2+2pq+2pr+2qr=m2,根据基本不等式得出2(p2+q2+r2)≥2pq+2pr+2qr,整体代入3(p2+q2+r2)≥${m}^{{\;}^{2}}$,得出3m≥m2,利用条件求解即可.
解答 解:∵p+q+r=m,且p2+q2+r2=m(m>0)
∴p+q=m-r,p2+q2=m-r2,
(1)当r=$\frac{1}{2}$,则pq=$\frac{1}{2}$[m2-2m$+\frac{1}{2}$],
p+q=m-$\frac{1}{2}$,
构造x2-(m-$\frac{1}{2}$)x$+\frac{1}{2}$[m2-2m$+\frac{1}{2}$]=0的两个不为0的根p,q,
∴△=(m-$\frac{1}{2}$)2-4×$\frac{1}{2}$[m2-2m$+\frac{1}{2}$]≥0,
即4m2-12m+3≤0,
m∈[$\frac{3-\sqrt{6}}{2}$,$\frac{3+\sqrt{6}}{2}$];
(2)当m=1时,p+q=1-r,p2+q2=1-r2,
pq=r2-r,
∴$\frac{1}{p}$+$\frac{1}{q}$=$\frac{p+q}{pq}$=$\frac{1-r}{{r}^{2}-r}$=$-\frac{1}{r}$,
构造x2-(1-r)x+(r2-r)=0的两个不为0的根p,q,
∴△=(1-r)2-4(r2-r)≥0,
即r∈[-$\frac{1}{3}$,0)∪(0,1],
∴$-\frac{1}{r}$∈[3,+∞)∪(-∞,-1],
∵$\frac{1}{p}+\frac{1}{q}$≠-1
$\frac{1}{p}$+$\frac{1}{q}$的取值范围:[3,+∞)∪(-∞,-1),
(3)∵p+q+r=m,且p2+q2+r2=m(m>0).
∴p2+q2+r2+2pq+2pr+2qr=m2,
2(p2+q2+r2)≥2pq+2pr+2qr,
∴3(p2+q2+r2)≥${m}^{{\;}^{2}}$,
即3m≥m2,
求解得出m≤3,
∵m>0,
∴m的取值范围:(0.3]
点评 本题考察了学生的恒等变形能力,方程数学,基本不等式的运用,对字母较多的式子,化简运算的能力.属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 | B. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | ||
| C. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≤2 | D. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 |
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
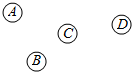 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )| A. | 8种 | B. | 12种 | C. | 16种 | D. | 20种 |