题目内容
已知函数
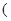 常数
常数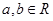 )满足
)满足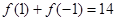 .
.
(1)求出 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;
(2)若 在区间
在区间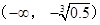 上单调递减,求
上单调递减,求 的最小值;
的最小值;
(3)在(2)的条件下,当 取最小值时,证明:
取最小值时,证明: 恰有一个零点
恰有一个零点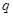 且存在递增的正整数数列
且存在递增的正整数数列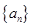 ,使得
,使得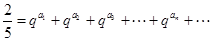 成立.
成立.
(1)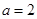 ,
,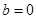 时是偶函数,
时是偶函数,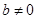 时,非奇非偶函数;(2)
时,非奇非偶函数;(2) ;(3)证明见解析.
;(3)证明见解析.
解析试题分析:(1)直接代入已知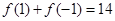 可求得
可求得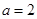 ,根据奇偶函数的定义可说明函数是奇(偶)函数,如果要说明它不是奇(偶)函数,可举例说明,即
,根据奇偶函数的定义可说明函数是奇(偶)函数,如果要说明它不是奇(偶)函数,可举例说明,即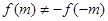 或
或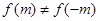 ;(2)据题意,即当
;(2)据题意,即当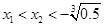 时,总有
时,总有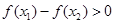 成立,变形整理可得
成立,变形整理可得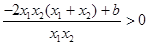 ,由于分母
,由于分母 ,故
,故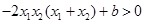 ,即
,即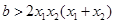 ,注意到
,注意到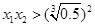 ,
,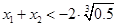 ,从而
,从而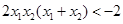 ,因此有
,因此有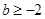 ;(3)在(2)的条件下,
;(3)在(2)的条件下,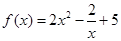 ,理论上讲应用求出零点
,理论上讲应用求出零点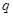 ,由函数表达式可看出,当
,由函数表达式可看出,当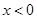 时,无零点,当
时,无零点,当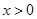 时,函数
时,函数 是递增函数,如有零点,只有一个,解方程
是递增函数,如有零点,只有一个,解方程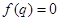 ,即
,即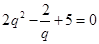 ,根据零点存在定理确定出
,根据零点存在定理确定出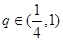 ,这个三次方程具体的解求不出,但可变形为
,这个三次方程具体的解求不出,但可变形为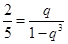 ,想到无穷递缩等比数列的和,有
,想到无穷递缩等比数列的和,有 ,因此可取
,因此可取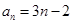 .证毕.
.证毕.
(1)由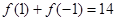 得
得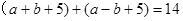 ,解得
,解得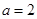 .
.
从而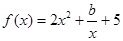 ,定义域为
,定义域为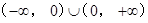
当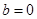 时,对于定义域内的任意
时,对于定义域内的任意 ,有
,有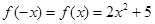 ,
, 为偶函数 2分
为偶函数 2分
当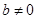 时,
时,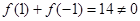 从而
从而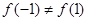 ,
, 不是奇函数;
不是奇函数;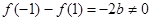 ,
, 不是偶函数,
不是偶函数,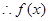 非奇非偶. 4分
非奇非偶. 4分
(2)对于任意的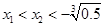 ,总有
,总有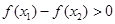 恒成立,即
恒成立,即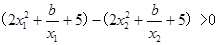 ,得
,得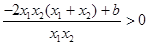 . 6分
. 6分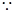
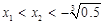 ,
,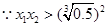 ,
,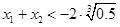 ,从而
,从而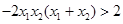 .
.
又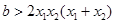 ,∴
,∴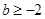 ,
, 的最小值等于
的最小值等于 . 10分
. 10分
(3)在(2)的条件下,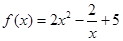 .
.
当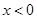 时,
时,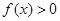 恒成立,函数
恒成立,函数 在
在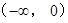 无零点. 12分
无零点. 12分
当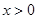 时,对于任意的
时,对于任意的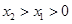 ,恒有
,恒有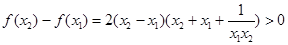 ,
,
即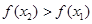 ,所以函数
,所以函数 在
在 上递增,又
上递增,又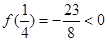 ,
,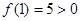 ,
,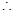
 在
在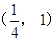 是有一个零点
是有一个零点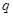 .
.
综上
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 定义域为
定义域为 .
. ,求实数
,求实数 的取值范围;
的取值范围; 在
在 上恒成立,求实数
上恒成立,求实数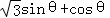 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.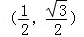 ,求f(θ)的值;
,求f(θ)的值;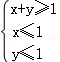 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.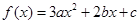 ,且有
,且有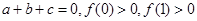 .
.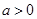 ,且
,且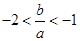 ;
; 在区间
在区间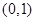 内有两个不同的零点.
内有两个不同的零点.
 的最小值;
的最小值; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,都有
,都有 成立.
成立.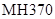 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线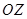 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
,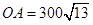 海里,且
海里,且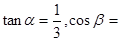
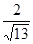 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口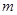 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛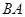 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线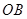 围成的三角形
围成的三角形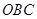 的面积
的面积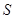 最小时,这种补给方案最优.
最小时,这种补给方案最优.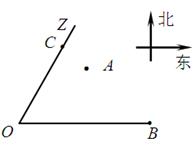
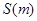 ;
; 为偶函数.
为偶函数. 的解析式;
的解析式;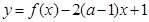 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数 的取值范围.
的取值范围.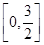 上的最大值.
上的最大值.