��Ŀ����
Ϊ��Ѱ������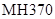 �к�,�ҹ���ѩ���š��ƿ�����2014��3��26�մӸۿ�
�к�,�ҹ���ѩ���š��ƿ�����2014��3��26�մӸۿ� �������ر�ƫ��
�������ر�ƫ�� �ǵ�����
�ǵ�����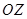 �����У����ڸۿڱ�ƫ��
�����У����ڸۿڱ�ƫ�� �ǵķ�������һ�����ƿ����������ʵ�С��
�ǵķ�������һ�����ƿ����������ʵ�С�� ��
��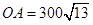 �����
�����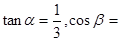
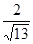 .��ָ�Ӳ���Ҫ��������λ�ڸۿ�
.��ָ�Ӳ���Ҫ��������λ�ڸۿ� ����
����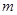 �����
����� ���IJ�������������
���IJ�����������С�� װ�ϲ������ʹ����ƿ������ô���
װ�ϲ������ʹ����ƿ������ô���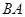 ����ȫ���Ͽƿ���������
����ȫ���Ͽƿ��������� �������������㵱�������еĺ����뺣����
�������������㵱�������еĺ����뺣����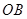 Χ�ɵ�������
Χ�ɵ������� �����
����� ��Сʱ�����ֲ�����������.
��Сʱ�����ֲ�����������.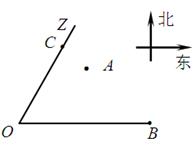
��1���� ����
����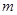 �ĺ�����ϵʽ
�ĺ�����ϵʽ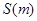 ��
��
��2��Ӧ����λ�ڸۿ��������ٺ��ﴦ�IJ�����ֻ�������������ţ�
��1��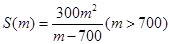 ����2��1400��
����2��1400��
���������������1��������֪������������Ϊ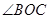 �ǹ̶��ģ���
�ǹ̶��ģ��� Ҳ�Dz��䣬ֱ��
Ҳ�Dz��䣬ֱ��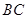 ����
���� ��Ҫ��
��Ҫ��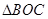 �������Сֵ��������֪�����������ý����������⣬��
�������Сֵ��������֪�����������ý����������⣬�� Ϊ����ԭ�㣬����Ϊ
Ϊ����ԭ�㣬����Ϊ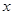 �����ᣬ����Ϊ
�����ᣬ����Ϊ �������ᣬ����ֱ������ϵ����ɵ�ֱ��
�������ᣬ����ֱ������ϵ����ɵ�ֱ��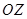 �ķ���Ϊ
�ķ���Ϊ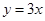 ����
���� ����Ϊ
����Ϊ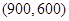 �����е�
�����е� ����Ϊ
����Ϊ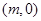 ���ɵ�ֱ��
���ɵ�ֱ��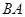 ���̣�����ֱ��
���̣�����ֱ��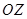 �Ľ���
�Ľ��� ������ɽ�ã���
������ɽ�ã��� ������Ҫ��ı���ʽ�Ϳɵã���2���ڣ�1�������ϣ�
������Ҫ��ı���ʽ�Ϳɵã���2���ڣ�1�������ϣ�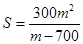 ������Сֵ���ѷ�ʽ�ķ��ӷ�ĸͬʱ����
������Сֵ���ѷ�ʽ�ķ��ӷ�ĸͬʱ����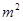 ����
����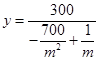 ����ĸ�ǹ���
����ĸ�ǹ���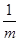 �Ķ��κ�������ֵ����.
�Ķ��κ�������ֵ����.
�����������1����O��Ϊԭ�㣬�����ķ���Ϊy����������ֱ������ϵ�� ��1�֣�
��ֱ��OZ�ķ���Ϊ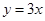 �����A��x0��y0������
�����A��x0��y0������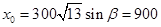 ��
��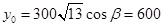 ����A��900��600���� ��3�֣�
����A��900��600���� ��3�֣�
��B��m��0������ֱ��AB�ķ���Ϊ��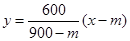 �� ��4�֣�
�� ��4�֣�
�ɴ˵õ�C������Ϊ��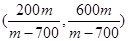 �� ��6�֣�
�� ��6�֣� ��8�֣�
��8�֣�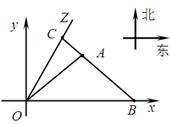
��2���ɣ�1��֪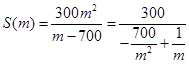 ��10�֣�
��10�֣�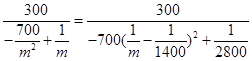 ��12�֣�
��12�֣�
���Ե�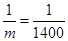 ����
����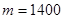 ʱ��
ʱ��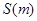 ��С��
����
������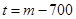 ����
����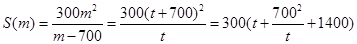
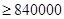 �����ҽ���
�����ҽ���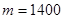 ʱ��
ʱ��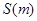 ��С��
����
������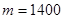 ���ﴦ�Ĵ�ֻʱ��������������. ��14�֣�
���ﴦ�Ĵ�ֻʱ��������������. ��14�֣�
���㣺��������Ӧ����.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� �DZ߳�Ϊ
�DZ߳�Ϊ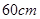 ��������ӲֽƬ����ȥ��Ӱ������ʾ���ĸ�ȫ�ȵĵ���ֱ�������Σ�������������ʹ��
��������ӲֽƬ����ȥ��Ӱ������ʾ���ĸ�ȫ�ȵĵ���ֱ�������Σ�������������ʹ�� �ĸ����غ���ͼ�еĵ�P�������γ�һ������������״�İ�װ�У�
�ĸ����غ���ͼ�еĵ�P�������γ�һ������������״�İ�װ�У� ��
�� ���DZ���ȥ�ĵ���ֱ��������б�ߵ������˵㣬��
���DZ���ȥ�ĵ���ֱ��������б�ߵ������˵㣬�� ��
�� �������
������� Ӧȡ��ֵ��
Ӧȡ��ֵ�� �������
�������


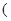 ����
����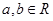 ������
������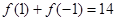 .
. ��ֵ�����ͳ���
��ֵ�����ͳ��� �IJ�ͬȡֵ���ۺ���
�IJ�ͬȡֵ���ۺ��� ��ż�ԣ�
��ż�ԣ�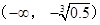 �ϵ����ݼ�����
�ϵ����ݼ�����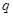 �Ҵ��ڵ���������������
�Ҵ��ڵ���������������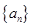 ��ʹ��
��ʹ��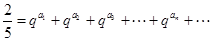 ����.
����.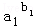
 ��
��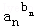 ��1��
��1�� ��
��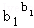
 ��
��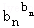 ��b12+b22+��+bn2��
��b12+b22+��+bn2�� ����0
����0
 �Ϻ������
�Ϻ������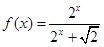 ��
��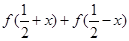 ��ֵ��
��ֵ�� �IJ���ʽ��
�IJ���ʽ��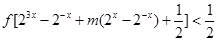 ������
������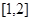 ���н⣬��ʵ��
���н⣬��ʵ��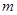 ��ȡֵ��Χ��
��ȡֵ��Χ�� ΪԲ�ĵ�����ͬ��Բ��
ΪԲ�ĵ�����ͬ��Բ�� ����
���� �Լ������߶�
�Լ������߶� ��
�� Χ�ɵķ��ͼ�Σ���̳����ܳ�Ϊ30�ף����д�Բ��
Χ�ɵķ��ͼ�Σ���̳����ܳ�Ϊ30�ף����д�Բ�� �ף�
�ף� ����Բ�Ľ�Ϊ
����Բ�Ľ�Ϊ ���ȣ�
���ȣ�
 ����
����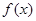 �����ڶ��������ʵ��
�����ڶ��������ʵ��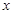 ������
������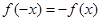 �����
�����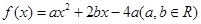 �����ж�
�����ж�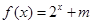 �Ƕ�����
�Ƕ�����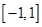 �ϵġ��ֲ��溯��������ʵ��
�ϵġ��ֲ��溯��������ʵ��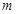 ��ȡֵ��Χ��
��ȡֵ��Χ��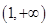 �Ϻ�ȡ��ֵ��
�Ϻ�ȡ��ֵ��