题目内容
(本小题满分14分)
已知函数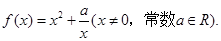
(Ⅰ)当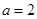 时,解不等式
时,解不等式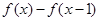 >
>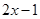 ;
;
(Ⅱ)讨论函数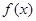 的奇偶性,并说明理由.
的奇偶性,并说明理由.
已知函数
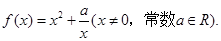
(Ⅰ)当
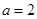 时,解不等式
时,解不等式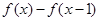 >
>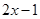 ;
;(Ⅱ)讨论函数
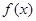 的奇偶性,并说明理由.
的奇偶性,并说明理由.(Ⅰ){x︱ <
<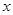 <1};(Ⅱ)
<1};(Ⅱ)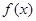 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
 <
<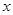 <1};(Ⅱ)
<1};(Ⅱ)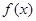 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数. 本试题主要是考查了函数中不等式的求解,以及奇偶性的判定的综合运用。
(1)根据已知解析式,可知函数当a=2时的表达式,然后解不等式,结合了一元二次不等式的思想来完成求解。
(2)先求解函数定义域,看看是否关于原点对称,然后利用奇偶性中函数的f(x)与f(-x)的关系得到结论。
解:(Ⅰ)当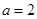 时,
时,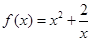 ,
,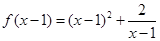 ,----------2分
,----------2分
由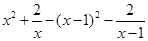 >
>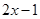 , 得
, 得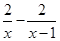 >
> ,------------4分
,------------4分
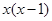 <
< ,
, <
<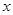 <
<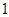 ------------------6分
------------------6分
∴原不等式的解为 {x︱ <
<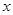 <1}; --------------7分
<1}; --------------7分
(Ⅱ)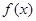 的定义域为
的定义域为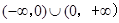 , ----------------8分
, ----------------8分
当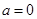 时,
时,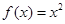 ,
,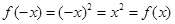 ,所以
,所以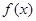 是偶函数.--------10分
是偶函数.--------10分
当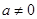 时,
时,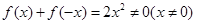 ,
, 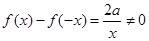 --------12分
--------12分
所以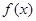 既不是奇函数,也不是偶函数. -------------14分
既不是奇函数,也不是偶函数. -------------14分
(1)根据已知解析式,可知函数当a=2时的表达式,然后解不等式,结合了一元二次不等式的思想来完成求解。
(2)先求解函数定义域,看看是否关于原点对称,然后利用奇偶性中函数的f(x)与f(-x)的关系得到结论。
解:(Ⅰ)当
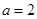 时,
时,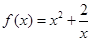 ,
,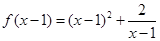 ,----------2分
,----------2分由
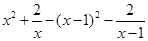 >
>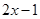 , 得
, 得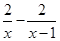 >
> ,------------4分
,------------4分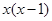 <
< ,
, <
<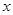 <
<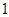 ------------------6分
------------------6分∴原不等式的解为 {x︱
 <
<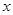 <1}; --------------7分
<1}; --------------7分 (Ⅱ)
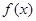 的定义域为
的定义域为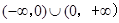 , ----------------8分
, ----------------8分当
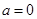 时,
时,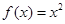 ,
,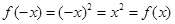 ,所以
,所以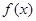 是偶函数.--------10分
是偶函数.--------10分 当
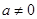 时,
时,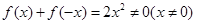 ,
, 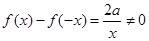 --------12分
--------12分 所以
 既不是奇函数,也不是偶函数. -------------14分
既不是奇函数,也不是偶函数. -------------14分 
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
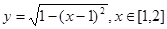 对于满足
对于满足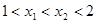 的任意
的任意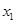 ,
,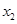 ,给出下列结论:
,给出下列结论: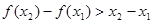 ; ②
; ②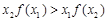 ;
;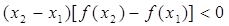 . ④
. ④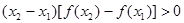
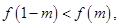 求实数m的取值范围.
求实数m的取值范围.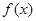 是定义在(0,+∞)上的单调增函数,满足:
是定义在(0,+∞)上的单调增函数,满足: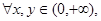 恒有
恒有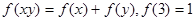 ,求:
,求: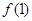 ;
;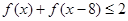 ,求
,求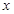 的取值范围。
的取值范围。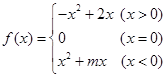 为奇函数,若函数
为奇函数,若函数 在区间
在区间 上单调递增,则
上单调递增,则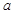 的取值范围是
的取值范围是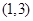
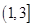
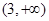
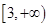
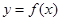 的反函数为
的反函数为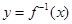 ,定义:若对给定的实数
,定义:若对给定的实数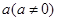 ,函数
,函数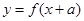 与
与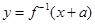 互为反函数,则称
互为反函数,则称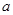 和性质”.
和性质”.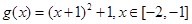 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;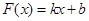 ,其中
,其中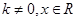 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得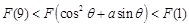 对任意的
对任意的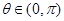 恒成立?若存在,求出
恒成立?若存在,求出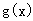 是
是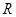 上的奇函数,且当
上的奇函数,且当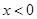 时
时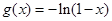 ,
,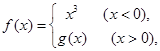 若
若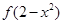 >
>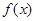 ,则实数
,则实数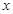 的取值范围是
的取值范围是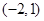
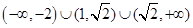
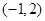
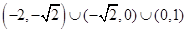
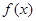 的图像关于
的图像关于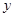 轴对称,又已知
轴对称,又已知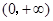 上为减函数,且
上为减函数,且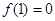 ,则不等式
,则不等式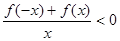 的解集为( )
的解集为( )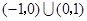
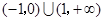
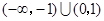
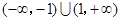
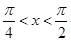 ,则函数
,则函数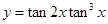 的最大值为 .
的最大值为 .