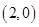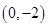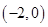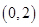题目内容
已知向量
=(1，-2)，
=(x，y)．
（Ⅰ）若x，y分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次时第一次，第二次出现的点数，求满足
•
=-1的概率；
（Ⅱ）若x，y∈[1，6]，求满足
•
＞0的概率．
| a |
| b |
（Ⅰ）若x，y分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次时第一次，第二次出现的点数，求满足
| a |
| b |
（Ⅱ）若x，y∈[1，6]，求满足
| a |
| b |
（Ⅰ）设（x，y）表示一个基本事件，
则抛掷两次骰子的所有基本事件有（1，1），（1，2），
（1，3），（1，4），（1，5），（1，6），（2，1），
（2，2），，（6，5），（6，6），共36个．（2分）
用A表示事件“
•
=-1”，即x-2y=-1
则A包含的基本事件有（1，1），（3，2），（5，3），共3个．
∴P（A）=
=
答：事件“
•
=-1”的概率为
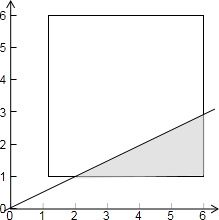
xyOOx=1Ox=6Oy=1Oy=6Ox-2y=0O
（Ⅱ）用B表示事件“
•
＞0”，即x-2y＞0
试验的全部结果所构成的区域为
{（x，y）|1≤x≤6，1≤y≤6}
构成事件B的区域为
{（x，y）|1≤x≤6，1≤y≤6，x-2y＞0}
如图所示：所以所求的概率为P（B）=
=
答：事件“
•
＞0”的概率为
则抛掷两次骰子的所有基本事件有（1，1），（1，2），
（1，3），（1，4），（1，5），（1，6），（2，1），
（2，2），，（6，5），（6，6），共36个．（2分）
用A表示事件“
| a |
| b |
则A包含的基本事件有（1，1），（3，2），（5，3），共3个．
∴P（A）=
| 3 |
| 36 |
| 1 |
| 12 |
答：事件“
| a |
| b |
| 1 |
| 12 |
xyOOx=1Ox=6Oy=1Oy=6Ox-2y=0O
（Ⅱ）用B表示事件“
| a |
| b |
试验的全部结果所构成的区域为
{（x，y）|1≤x≤6，1≤y≤6}
构成事件B的区域为
{（x，y）|1≤x≤6，1≤y≤6，x-2y＞0}
如图所示：所以所求的概率为P（B）=
| ||
| 5×5 |
| 4 |
| 25 |
答：事件“
| a |
| b |
| 4 |
| 25 |
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
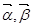是一组基底，向量
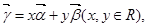则称
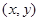为向量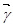
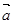在基底
在基底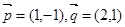
下的坐标为
，则向量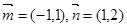
下的坐标为（ ）.
