题目内容
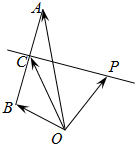
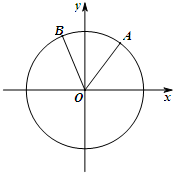
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
(Ⅰ)若点A的横坐标是
,点B的纵坐标是
,求sin(α+β)的值;
(Ⅱ)若|AB|=
,求
•
的值.
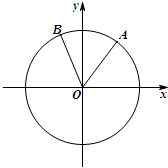
(Ⅰ)若点A的横坐标是
| 3 |
| 5 |
| 12 |
| 13 |
(Ⅱ)若|AB|=
| 3 |
| 2 |
| OA |
| OB |

(Ⅰ)根据三角函数的定义得,cosα=
,sinβ=
.…(2分)
∵α的终边在第一象限,∴sinα=
.…(3分)
∵β的终边在第二象限,∴cosβ=-
.…(4分)
∴sin(α+β)=sinαcosβ+cosαsinβ=
×(-
)+
×
=
.…(7分)
(Ⅱ)方法(1)∵|AB|=|
|=|
-
|,…(9分)
又∵|
-
|2=
2+
2-2
•
=2-2
•
,…(11分)
∴2-2
•
=
,
∴
•
=-
.…(13分)
方法(2)∵cos∠AOB=
=-
,…(10分)
∴
•
=|
||
|cos∠AOB=-
.…(13分)
| 3 |
| 5 |
| 12 |
| 13 |
∵α的终边在第一象限,∴sinα=
| 4 |
| 5 |
∵β的终边在第二象限,∴cosβ=-
| 5 |
| 13 |
∴sin(α+β)=sinαcosβ+cosαsinβ=
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
| 16 |
| 65 |
(Ⅱ)方法(1)∵|AB|=|
| AB |
| OB |
| OA |
又∵|
| OB |
| OA |
| OB |
| OA |
| OA |
| OB |
| OA |
| OB |
∴2-2
| OA |
| OB |
| 9 |
| 4 |
∴
| OA |
| OB |
| 1 |
| 8 |
方法(2)∵cos∠AOB=
| |OA|2+|OB|2-|AB|2 |
| 2|OA||OB| |
| 1 |
| 8 |
∴
| OA |
| OB |
| OA |
| OB |
| 1 |
| 8 |


练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
 =(5,1),
=(5,1),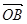 =(1,7),
=(1,7),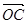 =(4,2),且
=(4,2),且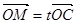 .
.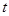 ,使
,使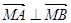 ?若存在,求出实数
?若存在,求出实数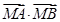 取最小值点M的坐标.
取最小值点M的坐标.