题目内容
16.过抛物线C:y2=4x上一点P(异于坐标原点O)作直线PA,交抛物线C于点A.(1)若直线PA过抛物线C的焦点,求$\overrightarrow{OA}$$•\overrightarrow{OP}$的值;
(2)过点P作直线PA的倾斜角互补的直线PB,交抛物线C于点B,设直线AB的斜率k1,抛物线C在点P处的切线斜率为k2,是否存在常数λ,使得k1=λk2?若存在,求λ的值;若不存在,说明理由;
(3)设直线PA过定点(1,0),过点A作与抛物线C在点P处的切线平行的直线l,交抛物线C于点Q,求△APQ面积的最小值.
分析 (1)设A(x1,y1),P(x0,y0),通过联立直线PA与抛物线方程,计算即得结论;
(2)通过分PA、PB的斜率存在与不存在两种情况讨论,利用根的判别式为0计算即得结论;
(3)通过联立直线AQ与抛物线方程,利用两点间距离公式、点到直线的距离公式及三角形面积公式计算即可.
解答 解:(1)设A(x1,y1),P(x0,y0),则直线PA的方程为:x=my+1,
联立$\left\{\begin{array}{l}{x=my+1}\\{{y}^{2}=4x}\end{array}\right.$,消去x整理得:y2-4my-4=0,
∴y1y0=-4,
∴$\overrightarrow{OA}$$•\overrightarrow{OP}$=x0x1+y1y0=$\frac{{{y}_{0}}^{2}{{y}_{1}}^{2}}{16}$+y1y0=1-4=-3;
(2)结论:存在常数λ=-1,使得k1=λk2.
理由如下:
设A(x1,y1),B(x2,y2),P(x0,y0),
当PA、PB的斜率存在时,由题可知:$\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}$+$\frac{{y}_{2}-{y}_{0}}{{x}_{2}-{x}_{0}}$=0,
即:$\frac{4}{{y}_{1}+{y}_{0}}$+$\frac{4}{{y}_{2}+{y}_{0}}$=0,即:y1+y2+2y0=0,
则k1=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{4}{{y}_{1}+{y}_{2}}$=-$\frac{2}{{y}_{0}}$,
联立$\left\{\begin{array}{l}{y-{y}_{0}={k}_{2}(x-{x}_{0})}\\{{y}^{2}=4x}\end{array}\right.$,消去x整理得:${y}^{2}-\frac{4}{{k}_{2}}y+\frac{4}{{y}_{0}}-4{x}_{0}=0$,
由△=0得:$\frac{16}{{{k}_{2}}^{2}}$-16($\frac{{y}_{0}}{{k}_{2}}$-x0)=0,
即$({y}_{0}{k}_{2}-2)^{2}=0$,即k2=$\frac{2}{{y}_{0}}$,则k1=-k2;
当PA、PB的斜率不存在时,显然满足k1=-k2;
故存在常数λ=-1,使得k1=λk2;
(3)直线AQ的方程为:y-y1=$\frac{2}{{y}_{0}}$(x-x1),
联立$\left\{\begin{array}{l}{y-{y}_{1}=\frac{2}{{y}_{0}}(x-{x}_{1})}\\{{y}^{2}=4x}\end{array}\right.$,消去x整理得:y2-2y0y-4x1-8=0,
|AQ|=$\sqrt{1+\frac{{{y}_{0}}^{2}}{4}}$•$\sqrt{4{{y}_{0}}^{2}+4(4{x}_{1}+8)}$=$\sqrt{4+{{y}_{0}}^{2}}$•$\sqrt{{{y}_{0}}^{2}+{{y}_{1}}^{2}+8}$=$\sqrt{4+{{y}_{0}}^{2}}$•|y0-y1|,
点P到直线AQ的距离d=$\frac{|\frac{2{x}_{0}}{{y}_{0}}-{y}_{0}-\frac{2{x}_{1}}{{y}_{0}}+{y}_{1}|}{\sqrt{1+\frac{4}{{{y}_{0}}^{2}}}}$=$\frac{|2{x}_{0}-{{y}_{0}}^{2}-2{x}_{1}-4|}{\sqrt{4+{{y}_{0}}^{2}}}$=$\frac{1}{2}$•$\frac{|{y}_{0}-{y}_{1}{|}^{2}}{\sqrt{4+{{y}_{0}}^{2}}}$,
∴S△APQ=$\frac{1}{4}$•$\sqrt{4+{{y}_{0}}^{2}}$•|y0-y1|•$\frac{|{y}_{0}-{y}_{1}{|}^{2}}{\sqrt{4+{{y}_{0}}^{2}}}$=$\frac{1}{4}$•$|{y}_{0}-{y}_{1}{|}^{3}$=$\frac{1}{4}$•$|{y}_{0}+\frac{1}{{y}_{0}}{|}^{3}$≥$\frac{1}{4}$•43=16,
当且仅当y0=±2时取等号,故△APQ面积的最小值为16.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查韦达定理、向量数量积运算、两点间距离公式、点到直线的距离公式、三角形面积公式等基础知识,注意解题方法的积累,属于中档题.

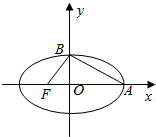 如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.
如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.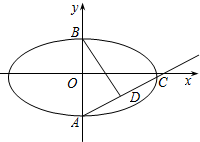 如图,A,B是椭圆W:$\frac{x^2}{3}$+y2=1的两个顶点,过点A的直线与椭圆W交于另一点C.
如图,A,B是椭圆W:$\frac{x^2}{3}$+y2=1的两个顶点,过点A的直线与椭圆W交于另一点C.