已知点A2+y2=5与椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一个公共点.若F1.F2分别是椭圆的左.右焦点.点P(4.4).且直线PF1与圆C相切．(1)求m的值与椭圆E的方程,(2)设Q为椭圆E上的一个动点.求$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值� 题目和参考答案——青夏教育精英家教网——

题目内容

19．已知点A（3，1）是圆C：（x-m）²+y²=5（m＜3）与椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个公共点，若F₁，F₂分别是椭圆的左、右焦点，点P（4，4），且直线PF₁与圆C相切．
（1）求m的值与椭圆E的方程；
（2）设Q为椭圆E上的一个动点，求$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值范围．

分析（1）通过将点A代入圆C方程，利用m＜3即得圆C方程，设直线PF₁：y=k（x-4）+4，通过直线PF₁与圆C相切可得斜率k的值，进而可得结论；
（2）设Q（x，y），通过$\overrightarrow{AP}•\overrightarrow{AQ}$=x+3y-6，利用基本不等式计算即得结论．

解答解：（1）点A（3，1）代入圆C方程得：（3-m）²+1=5．
∵m＜3，∴m=1，∴圆C：（x-1）²+y²=5．
设直线PF₁的斜率为k，则PF₁：y=k（x-4）+4，即kx-y-4k+4=0．
∵直线PF₁与圆C相切，∴$\frac{|k-0-4k+4|}{\sqrt{1+{k}^{2}}}$=$\sqrt{5}$．
解得k=$\frac{11}{2}$或k=$\frac{1}{2}$．
当k=$\frac{11}{2}$时，直线PF₁与x轴的交点横坐标为$\frac{36}{11}$，不合题意，舍去．
当k=$\frac{1}{2}$时，直线PF₁与x轴的交点横坐标为-4，
∴c=4，∴F₁（-4，0），F₂（4，0）．
∴2a=AF₁+AF₂=$5\sqrt{2}+\sqrt{2}$=6$\sqrt{2}$，即a=3$\sqrt{2}$，
∴a²=18，b²=2．
∴椭圆E的方程为：$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{2}=1$；
（2）$\overrightarrow{AP}$=（1，3），设Q（x，y），$\overrightarrow{AQ}$=（x-3，y-1），
∴$\overrightarrow{AP}•\overrightarrow{AQ}$=（x-3）+3（y-1）=x+3y-6．
∵$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{2}=1$，即x²+（3y）²=18，
而x²+（3y）²≥2|x|•|3y|，∴-3≤xy≤3．
则（x+3y）²=x²+（3y）²+6xy=18+6xy的取值范围是[0，36]．
∴x+3y的取值范围是[-6，6]．
∴$\overrightarrow{AP}•\overrightarrow{AQ}$=x+3y-6的取值范围是[-12，0]．

点评本题是一道直线与圆锥曲线的综合题，涉及到直线与圆相切、点到直线的距离、向量数量积运算、基本不等式等基础知识，注意解题方法的积累，属于中档题．

练习册系列答案

阅读导航系列答案

教材3D解读系列答案

通城学典默写能手系列答案

新中考仿真试卷系列答案

毕业总复习高分策略指导与实战训练系列答案

创优考100分系列答案

高分中考系列答案

金牌教辅培优优选卷期末冲刺100分系列答案

中考专项突破系列答案

全能金卷小学毕业升学全程总复习系列答案

相关题目

11．已知数列{a_n}的前n项和为S_n，且S_n=$\frac{3}{2}{n^2$+$\frac{1}{2}n$，递增的等比数列{b_n}满足b₁+b₄=18，b₂b₃=32，
（1）求a_n，b_n的通项公式；
（2）设c_n=a_nb_n，n∈N^*，求数列c_n的前n项和T_n．

10．过椭圆9x²+y²=1的一个焦点F₁的直线与椭圆交于A，B两点，则A与B和椭圆的另一个焦点F₂构成的三角形ABF₂的周长是（　　）

7．已知矩形ABCD的长AB=4，宽AD=3，将其沿对角线BD折起，得到四面体A-BCD，如图所示，给出下列结论：
①四面体A-BCD体积的最大值为$\frac{72}{5}$；
②四面体A-BCD外接球的表面积恒为定值；
③若E、F分别为棱AC、BD的中点，则恒有EF⊥AC且EF⊥BD；
④当二面角A-BD-C为直二面角时，直线AB、CD所成角的余弦值为$\frac{16}{25}$；
⑤当二面角A-BD-C的大小为60°时，棱AC的长为$\frac{14}{5}$．
其中正确的结论有②③④（请写出所有正确结论的序号）．

14．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），点A为右顶点，点B为上顶点，坐标原点O到直线AB的距离为$\frac{\sqrt{30}}{5}$c（其中c为半焦距），则椭圆的离心率e为$\frac{\sqrt{3}}{3}$．

4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）中，长轴长为2$\sqrt{2}$，离心率等于$\frac{\sqrt{2}}{2}$，
（1）求椭圆C的标准方程；
（2）直线l交椭圆于A、B两点，且AB的中点M为（$\frac{1}{2}$，$\frac{1}{2}$），求直线l的方程．

11．已知动点M到点F（0，1）的距离等于点M到直线y=-1的距离，点M的轨迹为C．
（Ⅰ）求轨迹C的方程；
（Ⅱ）设P为直线l：x-y-2=0上的点，过点P作曲线C的两条切线PA，PB，
（ⅰ）当点P（$\frac{1}{2}$，-$\frac{3}{2}$）时，求直线AB的方程；
（ⅱ）当点P（x₀，y₀）在直线l上移动时，求|AF|•|BF|的最小值．

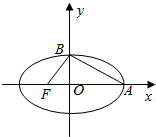如图所示，椭圆中心在坐标原点，F为左焦点，当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时，该椭圆被称为“黄金椭圆”，其离心率为$\frac{\sqrt{5}-1}{2}$，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$．

9．函数f（x）的定义域为[0，1），则f（1-3x）的定义域是（　　）

（-$\frac{1}{2}$，1]

（0，$\frac{1}{3}$]

（-$\frac{1}{3}$，0]