Question

【题目】已知函数，．

（Ⅰ）若在上存在极大值点，求实数的取值范围；

（Ⅱ）求证：，其中．

Answer 1

【答案】（Ⅰ） （Ⅱ）见证明

【解析】

（Ⅰ）先对函数求导，再由分类讨论的思想，分别讨论，和三种情况，即可得出结果；

（Ⅱ）令可得，由（Ⅰ）可知的极大值，再由时，，即可证明结论成立；也可用数学归纳法证明.

解：（Ⅰ）由于，

则①当时，，

即当时，，单调递增；

当时，，单调递减；

故在处取得极大值，

则，解得：；

②当时，恒成立，无极值，不合题意舍去；

③当时，，

即当时，，单调递减；

当时， ，单调递增；

故在处取得极小值，不合题意舍去；

因此当时，在上存在极大值点；

（Ⅱ）法一：令，，

由（Ⅰ）得：在处取得极大值1，且该极值是唯一的，

则，即，当且仅当时取“=”，

故当时，，

因此．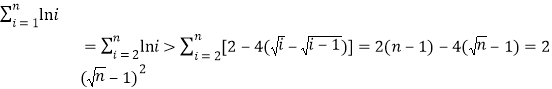

法二：下面用数学归纳法证明：，对恒成立．

（1）当时，左边，右边，

左边右边，结论成立；

（2）假设当时，结论成立，即，

当时，左边

，

而 ，

令，，

由（Ⅰ）得：在处取得极大值1，且该极值是唯一的，

则，即，当且仅当时取“=”，

则对恒成立，即

成立

故当时，结论成立，

因此，综合（1）（2）得，对恒成立