题目内容
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量 并有特征值λ2=-1及属于特征值-1的一个特征向量
并有特征值λ2=-1及属于特征值-1的一个特征向量 (1)求矩阵M.(2)求M5α.
(1)求矩阵M.(2)求M5α.
(1) (2)
(2)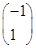
解析试题分析:(1)根据特征值λ1=4即特征向量 列出关于
列出关于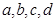 的方程组.同样根据特征值λ2=-1即特征向量
的方程组.同样根据特征值λ2=-1即特征向量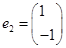 列出列出关于
列出列出关于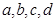 的方程组.通过解四元一次方程组可得
的方程组.通过解四元一次方程组可得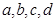 .从而求出矩阵M.
.从而求出矩阵M.
(2)由矩阵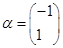 可表示为特征向量
可表示为特征向量
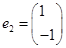 即
即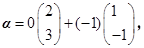 所以
所以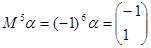 .即填
.即填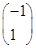 .
.
试题解析:(1)设M=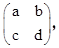
则 ∴
∴ ①
①
又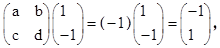 ∴
∴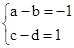 ②
②
由①②可得a=1,b=2,c=3,d=2,∴M= 4分
4分
(2)易知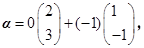 ∴
∴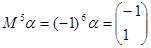 7分
7分
考点:1.矩阵的特征向量的表示.2.矩阵的乘法运算.

练习册系列答案
相关题目
 ,N=
,N= ,向量α=
,向量α= .
. 的特征值及对应的特征向量.
的特征值及对应的特征向量.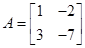 ,
,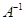 ;(2)若矩阵
;(2)若矩阵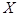 满足
满足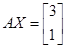 ,试求矩阵
,试求矩阵 ,绕原点逆时针旋转
,绕原点逆时针旋转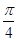 的变换所对应的矩阵为
的变换所对应的矩阵为 .
. :
: 在矩阵
在矩阵 对应变换作用下得到曲线
对应变换作用下得到曲线 ,求曲线
,求曲线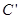 的方程.
的方程.
 不存在逆矩阵,求实数
不存在逆矩阵,求实数 的值及矩阵
的值及矩阵