题目内容
已知矩阵
，绕原点逆时针旋转
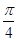的变换所对应的矩阵为
．
（Ⅰ）求矩阵；
（Ⅱ）若曲线
：
在矩阵
对应变换作用下得到曲线
，求曲线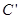
的方程．
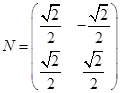（Ⅰ）
；（Ⅱ）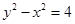
.
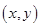解析试题分析：（1）（Ⅰ）根据旋转的角度求出矩阵；（Ⅱ）先根据坐标经过矩阵变换前后坐标
和坐标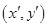 
之间的关系，然后用
、
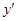来表示
、
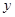，然后再将相应的结果代入曲线方程
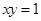并化简，便可得到变换后曲线的方程.
试题解析：（Ⅰ）由已知得，矩阵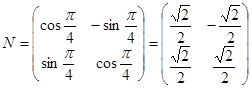
． 3分
（Ⅱ）矩阵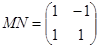
，它所对应的变换为
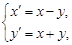解得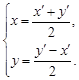
把它代人方程整理，得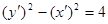
，
即经过矩阵变换后的曲线方程为
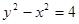. 7分
（注：先计算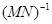
，再求曲线方程，可相应酌情给分）
考点：矩阵变换、坐标变换
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
用列举法表示集合{x|x∈N，x≤5}为（ ）
| A、{0，1，2，3，4} | B、{0，1，2，3，4，5} | C、{1，2，3，4} | D、{1，2，3，4，5} |
，B＝
，求矩阵A－1B.
并有特征值λ2=-1及属于特征值-1的一个特征向量
(1)求矩阵M.(2)求M5α.
，其对应的一个特征向量e=
，并且矩阵M对应的变换将点
变换成点
．
，若矩阵
所对应的变换把直线
：
变换为自身，求
．
成立的矩阵
．
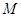，则
．