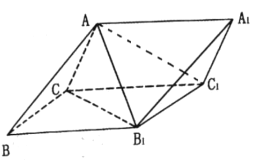
题目内容
【题目】已知F1 , F2分别是椭圆 ![]() 的左、右焦点F1 , F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点.
的左、右焦点F1 , F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点.
(1)求圆C的方程;
(2)设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a,b.当ab最大时,求直线l的方程.
【答案】
(1)解:由题意可知:F1(﹣2,0),F2(2,0).故⊙C的半径为2,圆心为原点O关于直线x+y﹣2=0的对称点.设圆心的坐标为(m,n).则 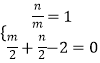 ,解得
,解得 ![]() .
.
∴圆C的方程为(x﹣2)2+(y﹣2)2=4;
(2)解:由题意,可设直线l的方程为x=my+2,则圆心到直线l的距离d= ![]() ,
,
∴b= ![]() .
.
由 ![]() 得(5+m2)y2+4my﹣1=0.
得(5+m2)y2+4my﹣1=0.
设l与E的两个交点分别为(x1,y1),(x2,y2).
则 ![]() ,
, ![]() .
.
∴a= ![]() =
= ![]() =
= ![]() ,
,
∴ab= ![]() =
= 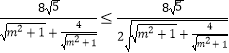 =
= ![]() .
.
当且仅当 ![]() ,即
,即 ![]() 时等号成立.
时等号成立.
故当 ![]() 时,ab最大,此时,直线l的方程为
时,ab最大,此时,直线l的方程为 ![]() ,即
,即 ![]() .
.
【解析】(1)由题意可知:F1(﹣2,0),F2(2,0),可得⊙C的半径为2,圆心为原点O关于直线x+y﹣2=0的对称点.设圆心的坐标为(m,n).利用线段的垂直平行的性质可得 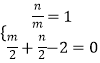 ,解出即可得到圆的方程;(2))由题意,可设直线l的方程为x=my+2,利用点到直线的距离公式可得圆心到直线l的距离d=
,解出即可得到圆的方程;(2))由题意,可设直线l的方程为x=my+2,利用点到直线的距离公式可得圆心到直线l的距离d= ![]() ,再利用弦长公式即可得到b=
,再利用弦长公式即可得到b= ![]() .把直线l的方程为x=my+2与椭圆的方程联立得到根与系数的关系,利用弦长公式即可得到a,进而得到ab,利用基本不等式的性质即可得出结论.
.把直线l的方程为x=my+2与椭圆的方程联立得到根与系数的关系,利用弦长公式即可得到a,进而得到ab,利用基本不等式的性质即可得出结论.
【考点精析】本题主要考查了圆的标准方程的相关知识点,需要掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程才能正确解答此题.
;圆心为A(a,b),半径为r的圆的方程才能正确解答此题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目