题目内容
【题目】设复数z=a+i(i是虚数单位,a∈R,a>0),且|z|=![]() .
.
(Ⅰ)求复数z;
(Ⅱ)在复平面内,若复数![]() +
+![]() (m∈R)对应的点在第四象限,求实数m取值范围.
(m∈R)对应的点在第四象限,求实数m取值范围.
【答案】解:(Ⅰ)∵z=a+i,|z|=![]() ,
,
∴|z|=![]() =
=![]() ,
,
即a2=9,解得a=±3,
又∵a>0,
∴a=3,…(5分)
∴z=3+i.
(Ⅱ)∵z=3+i,则![]() =3﹣i,
=3﹣i,
∴![]() +
+![]() =3﹣i+
=3﹣i+![]() =
=![]() +
+![]() i,
i,
又∵复数![]() +
+![]() (m∈R)对应的点在第四象限,
(m∈R)对应的点在第四象限,
∴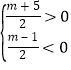 得
得![]()
∴﹣5<m<1.
【解析】(Ⅰ)根据复数的模长公式进行化简即可.
(Ⅱ)根据复数的几何意义进行化简求解.
【考点精析】解答此题的关键在于理解复数的乘法与除法的相关知识,掌握设![]() 则
则![]() ;
;![]() ,以及对复数的模(绝对值)的理解,了解复平面内复数所对应的点到原点的距离,是非负数,因而两复数的模可以比较大小;复数模的性质:(1)
,以及对复数的模(绝对值)的理解,了解复平面内复数所对应的点到原点的距离,是非负数,因而两复数的模可以比较大小;复数模的性质:(1)![]() (2)
(2)![]() (3)若
(3)若![]() 为虚数,则
为虚数,则![]() .
.

练习册系列答案
相关题目