题目内容
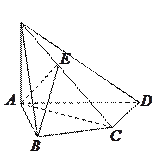
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意可得CD⊥平面PAC,结合线面垂直的定义即可得到AE⊥CD;
(Ⅱ)由题意可得AE⊥PD,AB⊥PD.利用线面垂直的判断定理可得证明![]() 平面
平面![]() ;
;
(Ⅲ)由题意找到二面角的平面角,结合三角形的边长关系可得二面角![]() 的大小是
的大小是![]() .
.
试题解析:
(I)证明:在四棱锥PABCD中,
因PA⊥底面ABCD,CD平面ABCD,故PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
而AE平面PAC,
∴AE⊥CD.
(II)证明:由PA=AB=BC,∠ABC=60,可得AC=PA.
∵E是PC的中点,∴AE⊥PC.
由(I)知,AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD.
而PD平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,PD在底面ABCD内射影是AD,AB⊥AD,∴AB⊥PD.
又AB∩AE=A,综上得PD⊥平面ABE.
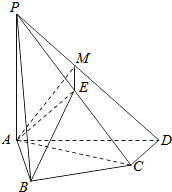
(III)过点A作AM⊥PD,垂足为M,连接EM.
由(II)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则EM⊥PD.
因此∠AME是二面角APDC的平面角。
由已知,得∠CAD=30°.设AC=a,可得![]() .
.
在Rt△ADP中,∵AM⊥PD,∴AM.PD=PA.AD.则![]() .
.
在Rt△AEM中, ![]() .
.
所以二面角APDC的大小是![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目