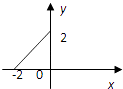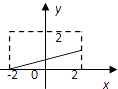题目内容
【题目】某种商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系式近似满足P= ![]() ,商品的日销售量Q(件)与时间t(天)的函数关系式近似满足Q=﹣t+40(1≤t≤30,t∈N).
,商品的日销售量Q(件)与时间t(天)的函数关系式近似满足Q=﹣t+40(1≤t≤30,t∈N).
(1)求这种商品日销售金额y与时间t的函数关系式;
(2)求y的最大值,并指出日销售金额最大的一天是30天中第几天.
【答案】
(1)解:设日销售金额为y元,则y=PQ,
即,y= ![]() ,t∈N
,t∈N
(2)解:当1≤t≤24时,y=﹣(t﹣10)2+900,
故当t=10时,ymax=900;
当25≤t≤30时,y=(t﹣70)2﹣900,
故当t=25时,ymax=1125.
故该商品日销售金额的最大值为1125元,且近30天中第25天销售金额最大
【解析】(1)设日销售金额为y元,则y=PQ,利用分段函数写出函数表达式;(2)当1≤t≤24时,y=﹣(t﹣10)2+900,当25≤t≤30时,y=(t﹣70)2﹣900,分别求最值,从而得到分段函数的最值及最值点.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目