题目内容
8.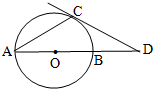 如图AB是圆O的直径,延长AB至D,使BD=OB,DC切圆O于C,则AC:AD=1:$\sqrt{3}$.
如图AB是圆O的直径,延长AB至D,使BD=OB,DC切圆O于C,则AC:AD=1:$\sqrt{3}$.
分析 连接OC、BC,利用切线的性质,圆的直径的性质,确定∠CAO=30°,即可得出结论.
解答  证明:连接OC、BC,
证明:连接OC、BC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵DC是⊙O的切线,
∴OC⊥DC,
∵BD=OB,
∴∠CDO=30°,
∴∠CAO=30°.
∴AC=$\frac{\sqrt{3}}{2}$AB,
∵AD=$\frac{3}{2}$AB,
∴AC:AD=1:$\sqrt{3}$.
故答案为:1:$\sqrt{3}$.
点评 本题考查了切线的性质,考查圆的直径的性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
18.直线$\sqrt{3}$x-y=0的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
13.△ABC中,角A,B,C的对边分别是a,b,c,a=1,b=$\sqrt{3}$,∠A=30°,则∠B等于( )
| A. | 60° | B. | 60°或120° | C. | 120° | D. | 无解 |