题目内容
已知双曲线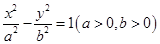 的左右顶点分别是
的左右顶点分别是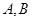 ,点
,点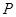 是双曲线上异于点
是双曲线上异于点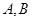 的任意一点。若直线
的任意一点。若直线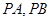 的斜率之积等于2,则该双曲线的离心率等于
的斜率之积等于2,则该双曲线的离心率等于
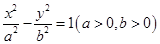 的左右顶点分别是
的左右顶点分别是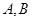 ,点
,点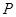 是双曲线上异于点
是双曲线上异于点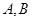 的任意一点。若直线
的任意一点。若直线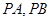 的斜率之积等于2,则该双曲线的离心率等于
的斜率之积等于2,则该双曲线的离心率等于 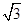
试题分析:利用斜率公式计算斜率,可得P的轨迹方程,即为双曲线方程,从而可求双曲线的离心率。设点P(x,y),则可知直线
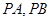 的斜率之积等于2,即为
的斜率之积等于2,即为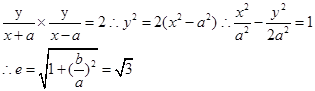
故答案为
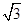
点评:本题考查双曲线的几何性质,考查学生分析解决问题的能力,属于中档题

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
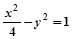 的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )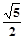
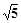
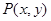 是抛物线
是抛物线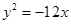 的准线与双曲线
的准线与双曲线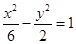 的两条渐近线所围成的三角形平面区域内(含边界)的任意一点,则
的两条渐近线所围成的三角形平面区域内(含边界)的任意一点,则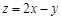 的最大值为_ __.
的最大值为_ __.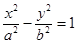 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆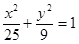 的焦点相同,求双曲线的方程及焦点坐标。
的焦点相同,求双曲线的方程及焦点坐标。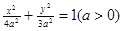 的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 . ,
,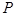 为
为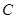 上任意一点;
上任意一点;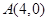 ,求
,求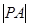 的最小值.
的最小值.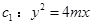 (
(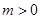 )的准线与
)的准线与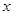 轴交于
轴交于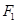 ,焦点为
,焦点为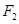 ;以
;以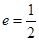 的椭圆
的椭圆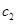 与抛物线
与抛物线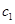 在
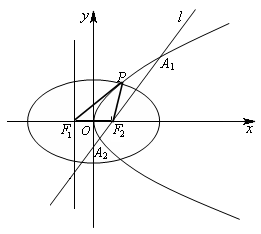
在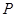 .
.
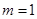 时,求椭圆的方程;
时,求椭圆的方程;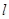 经过椭圆
经过椭圆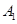 、
、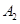 ,如果以线段
,如果以线段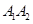 为直径作圆,试判断点
为直径作圆,试判断点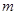 ,使得
,使得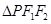 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 ,点
,点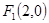 ,A
,A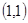 ,P为椭圆上任意一点,则
,P为椭圆上任意一点,则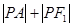 的取值范围是 。
的取值范围是 。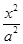 -
- =1的右焦点为
=1的右焦点为 ,则该双曲线的离心率等于( )
,则该双曲线的离心率等于( )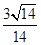 B.
B. C.
C. D.
D.