题目内容
如图,设抛物线 (
( )的准线与
)的准线与 轴交于
轴交于 ,焦点为
,焦点为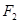 ;以
;以 、
、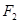 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线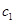 在
在 轴上方的一个交点为
轴上方的一个交点为 .
.

(1)当 时,求椭圆的方程;
时,求椭圆的方程;
(2)在(1)的条件下,直线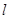 经过椭圆
经过椭圆 的右焦点
的右焦点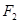 ,与抛物线
,与抛物线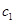 交于
交于 、
、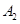 ,如果以线段
,如果以线段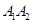 为直径作圆,试判断点
为直径作圆,试判断点 与圆的位置关系,并说明理由;
与圆的位置关系,并说明理由;
(3)是否存在实数 ,使得
,使得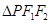 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
 (
( )的准线与
)的准线与 轴交于
轴交于 ,焦点为
,焦点为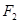 ;以
;以 、
、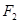 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线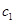 在
在 轴上方的一个交点为
轴上方的一个交点为 .
.
(1)当
 时,求椭圆的方程;
时,求椭圆的方程;(2)在(1)的条件下,直线
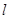 经过椭圆
经过椭圆 的右焦点
的右焦点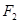 ,与抛物线
,与抛物线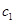 交于
交于 、
、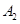 ,如果以线段
,如果以线段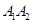 为直径作圆,试判断点
为直径作圆,试判断点 与圆的位置关系,并说明理由;
与圆的位置关系,并说明理由;(3)是否存在实数
 ,使得
,使得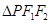 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.(1) (2)即点
(2)即点 可在圆内,圆上或圆外
可在圆内,圆上或圆外
(3) 时,能使
时,能使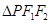 的边长是连续的自然数
的边长是连续的自然数
 (2)即点
(2)即点 可在圆内,圆上或圆外
可在圆内,圆上或圆外(3)
 时,能使
时,能使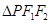 的边长是连续的自然数
的边长是连续的自然数解:∵
 的右焦点
的右焦点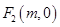 ∴椭圆的半焦距
∴椭圆的半焦距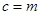 ,又
,又 ,
,∴椭圆的长半轴的长
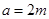 ,短半轴的长
,短半轴的长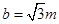 . 椭圆方程为
. 椭圆方程为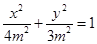 .
.(1)当
 时,故椭圆方程为
时,故椭圆方程为 , 3分
, 3分(2)依题意设直线
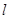 的方程为:
的方程为: ,
,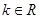
联立
 得点
得点 的坐标为
的坐标为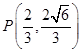 .
.将
 代入
代入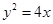 得
得 .
.设
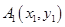 、
、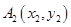 ,由韦达定理得
,由韦达定理得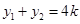 ,
,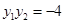 .
.又
 ,
, .
.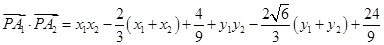
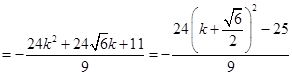
∵
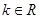 ,于是
,于是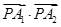 的值可能小于零,等于零,大于零。
的值可能小于零,等于零,大于零。即点
 可在圆内,圆上或圆外. ………………………………9分
可在圆内,圆上或圆外. ………………………………9分(3)假设存在满足条件的实数
 , 由
, 由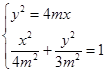 解得:
解得: .
.∴
 ,
,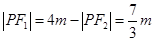 ,又
,又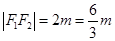 .
.即
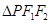 的边长分别是
的边长分别是 、
、 、
、 . ∴
. ∴ 时,能使
时,能使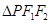 的边长是连续的自然数。 14分
的边长是连续的自然数。 14分 点评:解决该试题的关键是熟练的运用椭圆的简单几何性质来求解参数a,b,c的值,得到方程,并利用联立方程组的思想求解弦长,抛物线的定义是解决的关键点。属于基础题。

练习册系列答案
相关题目
 ,它的离心率为
,它的离心率为 ,一个焦点和抛物线
,一个焦点和抛物线 的焦点重合,过直线
的焦点重合,过直线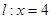 上一点
上一点 引椭圆
引椭圆 .
.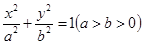 上的点
上的点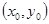 处的椭圆的切线方程是
处的椭圆的切线方程是 . 求证:直线
. 求证:直线 恒过定点
恒过定点 ;并出求定点
;并出求定点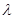 ,使得
,使得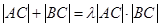 恒成立?(点
恒成立?(点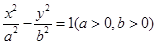 的右焦点
的右焦点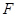 作圆
作圆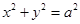 的切线
的切线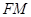 (切点为
(切点为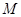 ),交
),交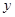 轴于点
轴于点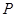 .若
.若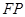 的中点,则双曲线的离心率为
的中点,则双曲线的离心率为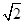
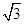
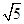
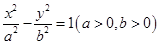 的左右顶点分别是
的左右顶点分别是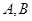 ,点
,点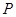 是双曲线上异于点
是双曲线上异于点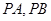 的斜率之积等于2,则该双曲线的离心率等于
的斜率之积等于2,则该双曲线的离心率等于 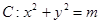 恰有三个点到直线
恰有三个点到直线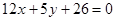 距离为
距离为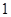 ,则
,则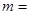 .
.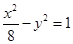 的右焦点为圆心,并与其渐近线相切的圆的标准方程是______
的右焦点为圆心,并与其渐近线相切的圆的标准方程是______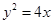 的焦点
的焦点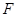 的直线交抛物线于
的直线交抛物线于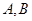 两点,满足
两点,满足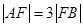 ,则弦
,则弦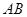 的中点到准线的距离为____.
的中点到准线的距离为____. 交于A,B两点,且
交于A,B两点,且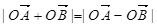 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )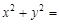 2
2 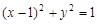
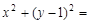 1
1 4
4