Question

【题目】已知函数 ， .
（1）若函数 在 上是减函数，求实数 的取值范围；
（2）是否存在整数 ，使得 的解集恰好是 ，若存在，求出 的值；若不存在，说明理由.

Answer 1

【答案】
（1）解：令 ，则 .
当 ，即 时， 恒成立，
所以 .
因为 在 上是减函数，
所以 ，解得 ，
所以 .
由 ，解得 或 .
当 时， 的图象对称轴 ，
且方程 的两根均为正，
此时 在 为减函数，所以 符合条件.
当 时， 的图象对称轴 ，
且方程 的根为一正一负，
要使 在 单调递减，则 ，解得 .
综上可知，实数 的取值范围为
（2）解：假设存在整数 ，使 的解集恰好是 ，则
①若函数 在 上单调递增，则 ， 且 ，
即
作差得到 ，代回得到： ，即 ，由于 均为整数，
故 ， ， 或 ， ， ，经检验均不满足要求；
②若函数 在 上单调递减，则 ， 且 ，
即
作差得到 ，代回得到： ，即 ，由于 均为整数，
故 ， ， 或 ， ， ，经检验均不满足要求；
③若函数 在 上不单调，则 ， 且 ，
即 作差得到 ，代回得到： ，即 ，由于 均为整数，
故 ， ， 或 ， ， ，，经检验均满足要求；
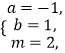综上：符合要求的整数 、 是 或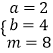
【解析】(1)首先求出对称轴根据题意分情况讨论区间在对称轴的右边，且f(0)不小于0以及区间在对称轴的左边，且f(0)不大于0，分别解出两种情况下的m的取值范围即可。(2)根据题意假设存在整数a、b使得 a ≤ f ( x ) ≤ b 的解集恰好是 [ a , b ] ，则 f ( a ) = a ， f ( b ) = b，代入数值求出a、b的值再代入到不等式检验即可。