题目内容
【题目】已知函数f(x)=  ,若f(x)的图象与直线y=kx有两个不同的交点,则实数k的取值范围
,若f(x)的图象与直线y=kx有两个不同的交点,则实数k的取值范围
【答案】![]()
【解析】作出f(x)的函数图象,如图所示: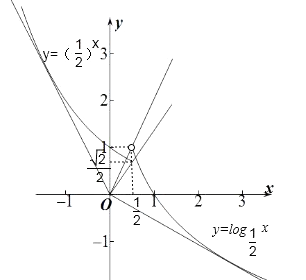
由图象可知当 ![]() 时,直线y=kx与f(x)的图象在第一象限有2个交点;
时,直线y=kx与f(x)的图象在第一象限有2个交点;
设直线y=k1x与y= ![]() 相切,切点为(a,b),
相切,切点为(a,b),
则 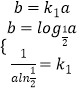 解得
解得 ![]() .
.
设直线y=k2x与y= ![]() 相切,切点为(m,n),
相切,切点为(m,n),
则 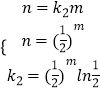 ,解得
,解得 ![]() ,
,
∴∴当 ![]() <k<0时,直线y=kx与f(x)的图象在第四象限有2个交点;
<k<0时,直线y=kx与f(x)的图象在第四象限有2个交点;
当k<eln2时,直线y=kx与f(x)的图象在第二象限有2个交点。
综上,k的取值范围是 ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了指数函数的图像与性质的相关知识点,需要掌握a0=1, 即x=0时,y=1,图象都经过(0,1)点;ax=a,即x=1时,y等于底数a;在0<a<1时:x<0时,ax>1,x>0时,0<ax<1;在a>1时:x<0时,0<ax<1,x>0时,ax>1才能正确解答此题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目