Question

【题目】已知直线l的参数方程为 （t为参数），在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线M的方程为ρ2（1+sin2θ）=1．
（1）求曲线M的直角坐标方程；
（2）若直线l与曲线M只有一个公共点，求倾斜角α的值．

Answer 1

【答案】
（1）解：曲线M的方程为ρ2（1+sin2θ）=1，

∵ρcosθ=x，ρsinθ=y，ρ2=x2+y2，

∴x2+2y2=1

（2）解：∵直线l的参数方程为 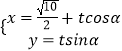（t为参数），

∴y=tanα（x﹣ ），

由 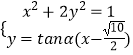，得：x2+2 ，

即（1+2tan2α）x2﹣2 tan2αx+5tan2α﹣1=0，

若直线l与曲线M只有一个公共点，

则△= ﹣4（1+2tan2α）（5tan2α﹣1）=0，

解得：tanα=± ，

∴α= 或

【解析】（1）利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2 ， 进行代换即可得出其直角坐标方程；（2）求出直线l的直角坐标方程，联立方程组，根据△=0，得到关于tanα的方程，解出即可．