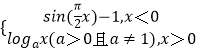题目内容
【题目】如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AC=1,PA=1,求圆心O到平面PBC的距离.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证明AC⊥BC,PA⊥BC,然后证明BC⊥平面PAC,转化证明平面PAC⊥平面PBC;
(2)过A点作AD⊥PC于点D,连BD,取BD的中点E,连OE,说明OE长就是O到平面PBC的距离,然后求解即可.
解:(1)证明:由AB是圆的直径得AC⊥BC,
由PA⊥平面ABC,BC平面ABC,得PA⊥BC
∴BC⊥平面PAC,
又∴BC平面PBC,
所以平面PAC⊥平面PBC
(2)过A点作AD⊥PC于点D,则由(1)知AD⊥平面PBC,
连BD,取BD的中点E,连OE,则OE∥AD,
又AD⊥平面PBCOE⊥平面PBC,
所以OE长就是O到平面PBC的距离.
由中位线定理得![]()

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).
编 号 | 分 组 | 频 数 |
1 | [0,2) | 12 |
2 | [2,4) | 16 |
3 | [4,6) | 34 |
4 | [6,8) | 44 |
续 表
编 号 | 分 组 | 频 数 |
5 | [8,10) | 50 |
6 | [10,12) | 24 |
7 | [12,14) | 12 |
8 | [14,16) | 4 |
9 | [16,18] | 4 |
合计 | 200 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.