题目内容
【题目】已知圆![]() ,点
,点![]() ,
,![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)已知过坐标原点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,若在曲线
两点,若在曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() 的中点为
的中点为![]() ,切点为
,切点为![]() ,连
,连![]() 、
、![]() ,则
,则![]() ,推出点
,推出点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,然后求解曲线
的椭圆,然后求解曲线![]() 方程;
方程;
(2)由椭圆的对称性知坐标原点![]() 为线段
为线段![]() 的中点,结合
的中点,结合![]() 可知
可知![]() ,然后分直线
,然后分直线![]() 与坐标轴重合与直线
与坐标轴重合与直线![]() 的斜率不为零两种情况讨论,在第一种情况下求出
的斜率不为零两种情况讨论,在第一种情况下求出![]() 的面积,在第二种情况下,设直线
的面积,在第二种情况下,设直线![]() 的方程为
的方程为![]() ,可得出直线
,可得出直线![]() 的方程为
的方程为![]() ,求出
,求出![]() 的面积关于
的面积关于![]() 的关系式,利用基本不等式可求得
的关系式,利用基本不等式可求得![]() 面积的最小值,比较大小后可得出结论.
面积的最小值,比较大小后可得出结论.
(1)设![]() 的中点为
的中点为![]() ,切点为
,切点为![]() ,连
,连![]() 、
、![]() ,则
,则![]() ,
,
取![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() ,故
,故![]() .
.
所以点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆.
的椭圆.
其中,![]() ,
,![]() ,则
,则![]() ,因此,曲线
,因此,曲线![]() 的标准方程为
的标准方程为![]() ;
;
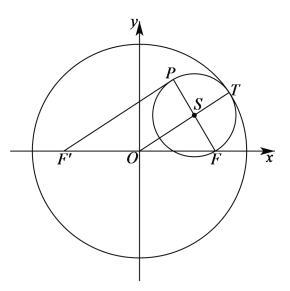
(2)![]() 过坐标原点
过坐标原点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,则坐标原点
两点,则坐标原点![]() 为线段
为线段![]() 的中点,
的中点,
![]() ,则
,则![]() .
.
①若直线![]() 与坐标轴重合,则
与坐标轴重合,则![]() 的面积为
的面积为![]() ;
;
②若直线![]() 的斜率不为零,设直线
的斜率不为零,设直线![]() 的方程为
的方程为![]() ,
,
联立![]() ,可得
,可得![]() ,所以,
,所以,![]() ,
,
同理可得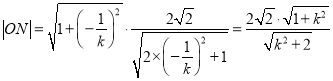 ,
,
此时,![]() 的面积为
的面积为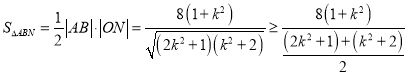
![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
![]() ,因此,
,因此,![]() 的面积的最小值为
的面积的最小值为![]() .
.

【题目】某企业现有A.B两套设备生产某种产品,现从A,B两套设备生产的大量产品中各抽取了100件产品作为样本,检测某一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是从A设备抽取的样本频率分布直方图,表1是从B设备抽取的样本频数分布表.
内的产品视为合格品,否则为不合格品.图1是从A设备抽取的样本频率分布直方图,表1是从B设备抽取的样本频数分布表.
图1:A设备生产的样本频率分布直方图
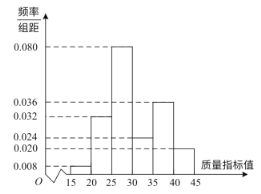
表1:B设备生产的样本频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计A.B设备生产的产品质量指标的平均值;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件利润240元;质量指标值落在
内的定为一等品,每件利润240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件利润180元;其它的合格品定为三等品,每件利润120元.根据图1、表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.企业由于投入资金的限制,需要根据A,B两套设备生产的同一种产品每件获得利润的期望值调整生产规模,请根据以上数据,从经济效益的角度考虑企业应该对哪一套设备加大生产规模?
内的定为二等品,每件利润180元;其它的合格品定为三等品,每件利润120元.根据图1、表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.企业由于投入资金的限制,需要根据A,B两套设备生产的同一种产品每件获得利润的期望值调整生产规模,请根据以上数据,从经济效益的角度考虑企业应该对哪一套设备加大生产规模?
【题目】为了了解一个智力游戏是否与性别有关,从某地区抽取男女游戏玩家各200请客,其中游戏水平分为高级和非高级两种.
(1)根据题意完善下列![]() 列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
性别 | 高级 | 非高级 | 合计 |
女 | 40 | ||
男 | 140 | ||
合计 |
(2)按照性别用分层抽样的方法从这些人中抽取10人,从这10人中抽取3人作为游戏参赛选手;
![]() 若甲入选了10人名单,求甲成为参赛选手的概率;
若甲入选了10人名单,求甲成为参赛选手的概率;
![]() 设抽取的3名选手中女生的人数为
设抽取的3名选手中女生的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附表: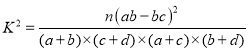 ,其中
,其中![]() .
.
| 0.010 | 0.05 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了100名高中生,根据问卷调查,得到以下数据:
作文成绩优秀 | 作文成绩一般 | 总计 | |
课外阅读量较大 | 35 | 20 | 55 |
课外阅读量一般 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.5%的把握认为课外阅读量的大小与作文成绩优秀有关;
(2)若用分层抽样的方式从课外阅读量一般的高中生中选取了6名高中生,再从这6名高中生中随机选取2名进行面谈,求面谈的高中生中至少有1名作文成绩优秀的概率.
附: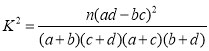 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |