ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΕ‘”Ύ’ΐ’ϊ ΐ![]() Θ§»γΙϊ
Θ§»γΙϊ![]() Ηω’ϊ ΐ
Ηω’ϊ ΐ![]() ¬ζΉψ
¬ζΉψ![]() Θ§
Θ§
«“![]() Θ§‘ρ≥Τ ΐΉι
Θ§‘ρ≥Τ ΐΉι![]() ΈΣ
ΈΣ![]() ΒΡ“ΜΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±.Φ«
ΒΡ“ΜΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±.Φ«![]() ΨυΈΣ≈Φ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΒΡΗω ΐΈΣ
ΨυΈΣ≈Φ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΒΡΗω ΐΈΣ![]() ΨυΈΣΤφ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΒΡΗω ΐΈΣ
ΨυΈΣΤφ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΒΡΗω ΐΈΣ![]() .
.
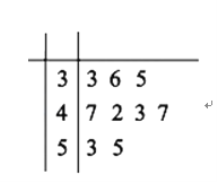
(Δώ)–¥≥ω’ϊ ΐ4ΒΡΥυ”–ΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±;
(Δρ)Ε‘”ΎΗχΕ®ΒΡ’ϊ ΐ![]() Θ§…η
Θ§…η![]() «
«![]() ΒΡ“ΜΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§«“
ΒΡ“ΜΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§«“![]() Θ§«σ
Θ§«σ![]() ΒΡΉν¥σ÷Β;
ΒΡΉν¥σ÷Β;
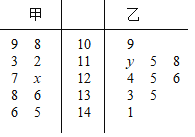
(Δσ)Ε‘Υυ”–ΒΡ’ΐ’ϊ ΐ![]() Θ§÷ΛΟς:
Θ§÷ΛΟς:![]() ;≤Δ«σ≥ω ΙΒΟΒ»Κ≈≥…ΝΔΒΡ
;≤Δ«σ≥ω ΙΒΟΒ»Κ≈≥…ΝΔΒΡ![]() ΒΡ÷Β.
ΒΡ÷Β.
(ΉΔ:Ε‘”Ύ![]() ΒΡΝΫΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±
ΒΡΝΫΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±![]() ”κ
”κ![]() Θ§Β±«“ΫωΒ±
Θ§Β±«“ΫωΒ±![]() «“
«“![]() ±Θ§≥Τ’βΝΫΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ± «œύΆ§ΒΡ.)
±Θ§≥Τ’βΝΫΗωΓΑ’ΐ’ϊ ΐΖ÷≤πΓ± «œύΆ§ΒΡ.)
ΓΨ¥πΑΗΓΩ(Δώ) ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜ(Δρ)
ΘΜ(Δρ) ![]() ΈΣ≈Φ ΐ ±Θ§
ΈΣ≈Φ ΐ ±Θ§![]() Θ§
Θ§![]() ΈΣΤφ ΐ ±Θ§
ΈΣΤφ ΐ ±Θ§![]() ΘΜ(Δσ)÷ΛΟςΦϊΫβΈωΘ§
ΘΜ(Δσ)÷ΛΟςΦϊΫβΈωΘ§![]() Θ§
Θ§![]()
ΓΨΫβΈωΓΩ
(Δώ)ΗυΨίΧβ“β÷±Ϋ”–¥≥ω¥πΑΗ.
(Δρ)Χ÷¬έΒ±![]() ΈΣ≈Φ ΐ ±Θ§
ΈΣ≈Φ ΐ ±Θ§![]() Ήν¥σΈΣ
Ήν¥σΈΣ![]() Θ§Β±
Θ§Β±![]() ΈΣΤφ ΐ ±Θ§
ΈΣΤφ ΐ ±Θ§![]() Ήν¥σΈΣ
Ήν¥σΈΣ![]() Θ§ΒΟΒΫ¥πΑΗ.
Θ§ΒΟΒΫ¥πΑΗ.
(Δσ) Χ÷¬έΒ±![]() ΈΣΤφ ΐ ±Θ§
ΈΣΤφ ΐ ±Θ§![]() Θ§÷Ν…Ό¥φ‘Ύ“ΜΗω»ΪΈΣ1ΒΡ≤πΖ÷Θ§Ι
Θ§÷Ν…Ό¥φ‘Ύ“ΜΗω»ΪΈΣ1ΒΡ≤πΖ÷Θ§Ι ![]() Θ§Β±
Θ§Β±![]() ΈΣ≈Φ ΐ ±Θ§
ΈΣ≈Φ ΐ ±Θ§
ΗυΨίΕ‘”ΠΙΊœΒΒΟΒΫ![]() Θ§‘ΌΦΤΥψ
Θ§‘ΌΦΤΥψ![]() Θ§
Θ§![]() Θ§ΒΟΒΫ¥πΑΗ.
Θ§ΒΟΒΫ¥πΑΗ.
(Δώ)’ϊ ΐ4ΒΡΥυ”–ΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
(Δρ)Β±![]() ΈΣ≈Φ ΐ ±Θ§
ΈΣ≈Φ ΐ ±Θ§![]() ±Θ§
±Θ§![]() Ήν¥σΈΣ
Ήν¥σΈΣ![]() ΘΜ
ΘΜ
Β±![]() ΈΣΤφ ΐ ±Θ§
ΈΣΤφ ΐ ±Θ§![]() ±Θ§
±Θ§![]() Ήν¥σΈΣ
Ήν¥σΈΣ![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘΚ![]() ΈΣ≈Φ ΐΘ§
ΈΣ≈Φ ΐΘ§![]() Ήν¥σΈΣ
Ήν¥σΈΣ![]() Θ§
Θ§![]() ΈΣΤφ ΐ ±Θ§
ΈΣΤφ ΐ ±Θ§![]() Ήν¥σΈΣ
Ήν¥σΈΣ![]() .
.
(Δσ)Β±![]() ΈΣΤφ ΐ ±Θ§
ΈΣΤφ ΐ ±Θ§![]() Θ§÷Ν…Ό¥φ‘Ύ“ΜΗω»ΪΈΣ1ΒΡ≤πΖ÷Θ§Ι
Θ§÷Ν…Ό¥φ‘Ύ“ΜΗω»ΪΈΣ1ΒΡ≤πΖ÷Θ§Ι ![]() ΘΜ
ΘΜ
Β±![]() ΈΣ≈Φ ΐ ±Θ§…η
ΈΣ≈Φ ΐ ±Θ§…η![]() «ΟΩΗω ΐΨυΈΣ≈Φ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§
«ΟΩΗω ΐΨυΈΣ≈Φ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§
‘ρΥϋ÷Ν…ΌΕ‘”ΠΝΥ![]() ΚΆ
ΚΆ![]() ΒΡΨυΈΣΤφ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§
ΒΡΨυΈΣΤφ ΐΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§
Ι ![]() .
.
Ήέ…œΥυ ωΘΚ![]() .
.
Β±![]() ±Θ§≈Φ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ
±Θ§≈Φ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ![]() Θ§Τφ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ
Θ§Τφ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Β±![]() ±Θ§≈Φ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ
±Θ§≈Φ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ![]() Θ§
Θ§![]() Θ§Τφ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ
Θ§Τφ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±ΈΣ![]() Θ§
Θ§![]()
Ι ![]() ΘΜ
ΘΜ
Β±![]() ±Θ§Ε‘”Ύ≈Φ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§≥ΐΝΥΗςœν≤Μ»ΪΈΣ
±Θ§Ε‘”Ύ≈Φ ΐΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§≥ΐΝΥΗςœν≤Μ»ΪΈΣ![]() ΒΡΤφ ΐ≤πΖ÷ΆβΘ§÷Ν…ΌΕύ≥ω“ΜœνΗςœνΨυΈΣ
ΒΡΤφ ΐ≤πΖ÷ΆβΘ§÷Ν…ΌΕύ≥ω“ΜœνΗςœνΨυΈΣ![]() ΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§Ι
ΒΡΓΑ’ΐ’ϊ ΐΖ÷≤πΓ±Θ§Ι ![]() .
.
Ήέ…œΥυ ωΘΚ Ι![]() ≥…ΝΔΒΡ
≥…ΝΔΒΡ![]() ΈΣΘΚ
ΈΣΘΚ![]() Μρ
Μρ![]() .
.

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ