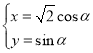题目内容
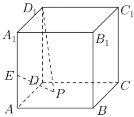
【题目】如图,正方体![]() 是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知
是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知![]() 为柱
为柱![]() 上一点(不在点
上一点(不在点![]() 、
、![]() 处),
处),![]() (
(![]() ),菜农需要在地面正方形
),菜农需要在地面正方形![]() 内画出一条曲线
内画出一条曲线![]() 将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点
将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点![]() 为地面正方形
为地面正方形![]() 内的曲线
内的曲线![]() 上任意一点,设
上任意一点,设![]() 、
、![]() 分别为在
分别为在![]() 点处观测
点处观测![]() 和
和![]() 的仰角.
的仰角.
(1)若![]() ,请说明曲线
,请说明曲线![]() 是何种曲线,为什么?
是何种曲线,为什么?
(2)若![]() 为柱
为柱![]() 的中点,且
的中点,且![]() 时,请求出点
时,请求出点![]() 所在区域的面积.
所在区域的面积.
【答案】(1)![]() ,圆的一部分;见解析(2)
,圆的一部分;见解析(2)![]()
【解析】
(1)平面![]() 中,以
中,以![]() 为原点,以
为原点,以![]() 为
为![]() 轴建立平面直角坐标系,设
轴建立平面直角坐标系,设![]() ,由
,由![]() 可得
可得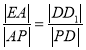 ,从而可求出轨迹方程.
,从而可求出轨迹方程.
(2)由![]() 可得
可得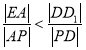 ,结合
,结合![]() 为柱
为柱![]() 的中点可求出
的中点可求出![]() 在正方形内部,且在
在正方形内部,且在![]() 内,结合图形,利用间接法求出区域面积.
内,结合图形,利用间接法求出区域面积.
(1)解:在平面![]() 中,以
中,以![]() 为原点,以
为原点,以![]() 为
为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,
则![]() ,由
,由![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,可知
,可知![]() .
.
则![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,
所以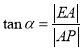 ,
,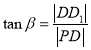 ,又
,又![]() ,则
,则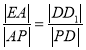 ,
,
所以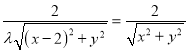 ,整理得,
,整理得,![]() ,
,
所以曲线![]() 是圆的一部分.
是圆的一部分.

(2)由![]() ,且均为锐角,则
,且均为锐角,则![]() ,由题意知,
,由题意知,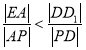 ,由
,由![]() ,
,
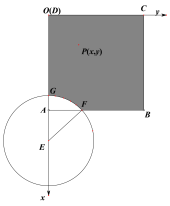
则![]() 在正方形内部,且在
在正方形内部,且在![]() 内,点
内,点![]() 所在区域如图阴影所示
所在区域如图阴影所示
圆的圆心为![]() ,半径
,半径![]() .
.![]() ,所以
,所以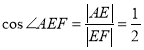 ,
,
所以![]() ,
,![]() ,所以扇形面积
,所以扇形面积![]() ,
,
又![]() ,
,
则阴影的面积![]() .
.

【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
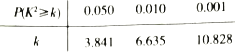 .
.