题目内容
9.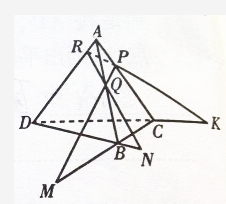 在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.
在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.
分析 由已知条件推导出M,N,K都在在平面PQR与平面BCD的交线上,由此能证明M,N,K三点共线.
解答 证明:∵M∈PQ,PQ?面PQR,M∈BC,BC?面BCD,
∴M是平面PQR与平面BCD的一个公共点
即M在平面PQR与平面BCD的交线上.
同理可证N,K也在该交线上.
∴M,N,K三点共线.
点评 本题考查三点共线的证明,是基础题,利用两平面交线的唯一性,是证明多点共线的常用方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.若a<1,b>1,那么下列命题中正确的是( )
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | $\frac{b}{a}$>1 | C. | a2<b2 | D. | ab<a+b |
18.已知函数f(x)=$\frac{3-m•{3}^{x}}{{3}^{x}}$,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[-$\frac{1}{4}$,1]上的最大值为2,若对任意x1∈[-1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
| A. | (-∞,-$\frac{2}{3}$] | B. | (-∞,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | [-$\frac{1}{3}$,+∞] |
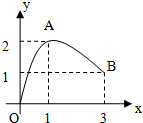 如图,函数f(x)的图象是曲线段OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[$\frac{1}{f(3)}$]的值为2.
如图,函数f(x)的图象是曲线段OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[$\frac{1}{f(3)}$]的值为2.